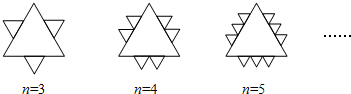题目内容
已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图示)。当n=8时,共向外做出了 18个
小等边三角形; 当n=k时,共向外做出了 3(k-2)个小等边三角形,这些小等边角形的面积和是 3(k-2)k2S(用含k的式子表示)。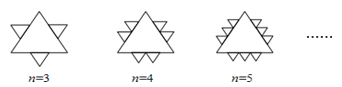
18 3(k-2) 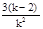 S
S
解析考点:等边三角形的性质;相似三角形的判定与性质.
分析:根据前三个图形小等边三角形的个数,推出n=8时共向外作出了18个等边三角形,归纳总结出第k个图形即n=k时,共向外作出的小等边三角形的个数,然后利用相似三角形的面积之比等于相似比的平方求出一个小等边三角形的面积,根据归纳出的个数即可求出所有小等边三角形的面积之和.
解:由第1个图形可知:n=3时,共向外作出了3(3-2)个三角形;
由第2个图形可知:n=4时,共向外作出了3(4-2)个三角形;
…
所以当n=8时,共向外作出了3(8-2)=18个三角形;
当n=k时,共向外作出了3(k-2)个三角形;
又第k个图形中的每一个小三角形都与最大的等边三角形相似,相似比为1:k,
所以面积比为1:k2,且最大的等边三角形的面积为S,
则一个小等边三角形的面积为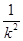 S,
S,
所以这些小等边三角形的面积和是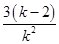 S.
S.
故答案为:18;3(k-2);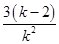 S.
S.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
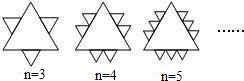
 已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图所示).当n=k时,向外作出的这些小等边三角形的面积和为
已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图所示).当n=k时,向外作出的这些小等边三角形的面积和为