题目内容
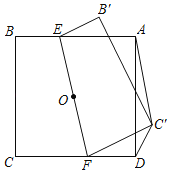
【题目】如图,在同一平面内,点O为正方形ABCD对角线交点,过点O折叠正方形,使C、C′两点重合,EF是折痕,连接AC′、DC′,若DC′=![]() ,AC′=6,则AD的长是_____.
,AC′=6,则AD的长是_____.
【答案】5![]()
【解析】
由正方形的性质和折叠的性质可得AO=CO=DO=C'O,∠ACD=45°,可证点A,点C',点C,点D在以点O为圆心的圆上,可得∠C=∠AC'M=45°,即可求AM=C'M的长,由勾股定理可求AD的长.
解:如图,连接AC,BD,过点A作AM⊥DC',

由折叠可得OC=OC',
∵点O为正方形ABCD对角线交点,
∴AO=CO=DO=C'O,∠ACD=45°,
∴点A,点C',点C,点D在以点O为圆心的圆上,
∴∠C=∠AC'M=45°,且AM⊥DC',AC'=6,
∴AM=C'M=3![]() ,
,
∴DM=4![]() ,
,
∵AD=![]() =
=![]() =5
=5![]()
故答案为:5![]() .
.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目