题目内容
小明看到一列数：1，1，-2，3，5，-8，13，21，-34，…，他想当前n项和第一次大于1000时，第n项应为多少？你知道答案吗？请写出________．
17
分析：根据斐波那契数列的通项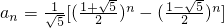
，通过通项或者一项一项加，可得1，1，-2，3，5，-8，13，21，-34，55，89，-144，233，377，-610，987，1597，从而求解．
解答：首先将所有的数都用来计算，可得从第三项开始，每一项都是前面两项的和；然后将所有的第3的倍数项加上负号即可，比如2变为-2，8变成-8，
以此类推通过通项或者一项一项加，可以得出正确答案是第17项1597．
故答案为：17．
点评：考查了规律型：数字的变化类，熟悉斐波那契数列的通项是解题的关键．
分析：根据斐波那契数列的通项
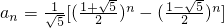，通过通项或者一项一项加，可得1，1，-2，3，5，-8，13，21，-34，55，89，-144，233，377，-610，987，1597，从而求解．解答：首先将所有的数都用来计算，可得从第三项开始，每一项都是前面两项的和；然后将所有的第3的倍数项加上负号即可，比如2变为-2，8变成-8，
以此类推通过通项或者一项一项加，可以得出正确答案是第17项1597．
故答案为：17．
点评：考查了规律型：数字的变化类，熟悉斐波那契数列的通项是解题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目