题目内容
 如图,在等边△ABC中,以AB为直径的⊙O与BC相交于点D,连接AD,则∠DAC的度数为
如图,在等边△ABC中,以AB为直径的⊙O与BC相交于点D,连接AD,则∠DAC的度数为分析:由于AB是直径,根据圆周角定理可知∠ADB是直角,即AD⊥BC;根据等边三角形三线合一的性质知,DA是∠BAC的角平分线,由此可求得∠DAC的度数.
解答:解:∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC;
又∵△ABC是等边三角形,
∴DA平分∠BAC,即∠DAC=
∠BAC=30°.
∴∠ADB=90°,即AD⊥BC;
又∵△ABC是等边三角形,
∴DA平分∠BAC,即∠DAC=
| 1 |
| 2 |
点评:此题主要考查了等边三角形的性质及圆周角定理的推论;
圆周角定理的推论:半圆(弧)和直径所对的圆周角是直角;
等边三角形三线合一:等边三角形每条边上的中线、高线和所对角的平分线互相重合.
圆周角定理的推论:半圆(弧)和直径所对的圆周角是直角;
等边三角形三线合一:等边三角形每条边上的中线、高线和所对角的平分线互相重合.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
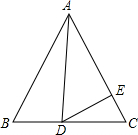 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
 16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是
16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是 21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.
21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°. 如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm.
如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm. 如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证:
如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证: