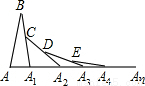
题目内容
如图，在△ABA1中，∠B=20°，AB=A1B，在A1B上取一点C，延长AA1到A2，使得A1A2=A1C；在A2C上取一点D，延长A1A2到A3，使得A2A3=A2D；…，按此做法进行下去，∠An的度数为 ▲ ．
【答案】
。
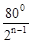【解析】先根据等腰三角形的性质求出∠BA1A的度数，再根据三角形外角的性质及等腰三角形的性质分别求出∠CA2A1，∠DA3A2及∠EA4A3的度数，找出规律即可得出∠An的度数：
∵在△ABA1中，∠B=20°，AB=A1B，∴∠BA1A=
。
∵A1A2=A1C，∠BA1A是△A1A2C的外角，∴∠CA2A1=
。
同理可得，∠DA3A2=20°，∠EA4A3=10°，······
∴∠An=。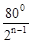
练习册系列答案
阅读快车系列答案
相关题目
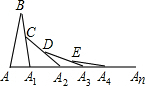（2012•贵阳）如图，在△ABA1中，∠B=20°，AB=A1B，在A1B上取一点C，延长AA1到A2，使得A1A2=A1C；在A2C上取一点D，延长A1A2到A3，使得A2A3=A2D；…，按此做法进行下去，∠An的度数为
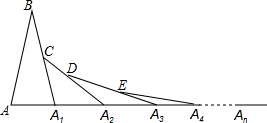如图，在△ABA1中，∠B=20°，AB=A1B，在A1B上取一点C，延长AA1到A2，使得A1A2=A1C得到第1个三角形；在A2C取一点D，延长A1A2到A3，使得A2A3=A2D，得到第2个三角形；…，按此做法进行下去，则：
如图，在△ABA1中，∠B=20°，AB=A1B，在A1B上取一点B1，延长AA1到A2，使A1A2=A1B1，在A2B1上取一点B2，延长到A1A2到A3，使A2A3=A2B2；…按此方法进行下去，∠An-1AnBn-1的度数为