题目内容
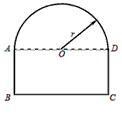
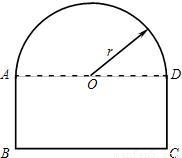
 一条隧道的截面如图所示,它的上部是一个以AD为直径的半圆O,下部是一个矩形ABCD.
一条隧道的截面如图所示,它的上部是一个以AD为直径的半圆O,下部是一个矩形ABCD.(1)当AD=4米时,求隧道截面上部半圆O的面积;
(2)已知矩形ABCD相邻两边之和为8米,半圆O的半径为r米.
①求隧道截面的面积S(米2)关于半径r(米)的函数关系式(不要求写出r的取值范围);
②若2米≤CD≤3米,利用函数图象求隧道截面的面积S的最大值(π取3.14,结果精确到0.1米).
分析:(1)已知直径求半圆面积,简单;
(2)截面面积=半圆面积+矩形面积.分别用含r的式子表示两个部分的面积可得函数关系式,根据关系式画图回答问题.
(2)截面面积=半圆面积+矩形面积.分别用含r的式子表示两个部分的面积可得函数关系式,根据关系式画图回答问题.
解答:解:(1)当AD=4米时,
S半圆=
π×(
)2=
π×22
=2π(米2).(3分)
(2)①∵AD=2r,AD+CD=8
∴CD=8-AD=8-2r(4分)
∴S=
πr2+AD•CD=
π r2+2r(8-2r)
=(
π-4)r2+16r.(8分)
②由①知CD=8-2r,
又∵2≤CD≤3,
∴2≤8-2r≤3,
∴2.5≤r≤3.(9分)
由①知S=(
π-4)r2+16r≈(
×3.14-4)r2+16r
=-2.43r2+16r(10分)
=-2.43(r-
)2+
∵-2.43<0,
∴函数图象为开口向下的抛物线.
∵函数对称轴r=
≈3.3(11分)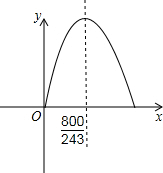
又因为2.5≤r≤3<3.3,
由函数图象知,其图象在对称轴左侧,函数为增函数,即S随r的增大而增大,
故当r=3时,有S最大值.(12分)
S最大值=(
π-4)×32+16×3
≈(
×3.14-4)×9+48
=26.13
≈26.1(米2)
答:隧道截面的面积S的最大值约为26.1米2.(13分)
S半圆=
| 1 |
| 2 |
| AD |
| 2 |
| 1 |
| 2 |
=2π(米2).(3分)
(2)①∵AD=2r,AD+CD=8
∴CD=8-AD=8-2r(4分)
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
=(
| 1 |
| 2 |
②由①知CD=8-2r,
又∵2≤CD≤3,
∴2≤8-2r≤3,
∴2.5≤r≤3.(9分)
由①知S=(
| 1 |
| 2 |
| 1 |
| 2 |
=-2.43r2+16r(10分)
=-2.43(r-
| 800 |
| 243 |
| 600 |
| 243 |
∵-2.43<0,
∴函数图象为开口向下的抛物线.
∵函数对称轴r=
| 8 |
| 2.43 |

又因为2.5≤r≤3<3.3,
由函数图象知,其图象在对称轴左侧,函数为增函数,即S随r的增大而增大,
故当r=3时,有S最大值.(12分)
S最大值=(
| 1 |
| 2 |
≈(
| 1 |
| 2 |
=26.13
≈26.1(米2)
答:隧道截面的面积S的最大值约为26.1米2.(13分)
点评:此题的最后一个问题应注意函数自变量的取值范围,在此范围内通过观察图象求出最值,往往并非是函数的最值.

练习册系列答案
相关题目
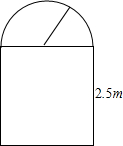
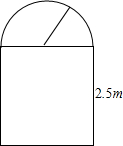 一条隧道的截面如图所示,它的上部是一个半圆,下部是一个矩形,矩形的一边长为2.5m.
一条隧道的截面如图所示,它的上部是一个半圆,下部是一个矩形,矩形的一边长为2.5m.