题目内容
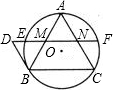 如图,⊙O是等边△ABC的外接圆,AB=2,M、N分别是边AB、AC的中点,直线MN交⊙O于E、F两点,BD∥AC交直线MN于点D.求出图中线段DM上已有的一条线段的长.
如图,⊙O是等边△ABC的外接圆,AB=2,M、N分别是边AB、AC的中点,直线MN交⊙O于E、F两点,BD∥AC交直线MN于点D.求出图中线段DM上已有的一条线段的长.
分析:连接OA交MN于点G,则OA⊥BC,由三角形的中位线的性质可得MN的长,易证得△BMD≌△AMN,有DM=MN,由相交弦定理得ME•MF=MA•MB,就可求得EM,DE的值.
解答: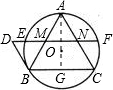 解:∵M,N分别是边AB,AC的中点
解:∵M,N分别是边AB,AC的中点
∴MN∥BC,MN=
BC=1
又∵BD∥AC
∴∠DBA=∠A=60°
∵BM=AM,∠BMD=∠AMN
∴△BMD≌△AMN
∴DM=MN=1
连接OA交MN于点G,则OA⊥BC
∴OA⊥EF
∴EG=FG,MG=FN
由相交弦定理得:ME•MF=MA•MB
∴EM(EM+1)=1
解得EM=
(EM=
不合题意,舍去)
∴DE=DM-EM=
∴DE(3-DE)=1
解得DE=
(DE=
不合题意,舍去).
 解:∵M,N分别是边AB,AC的中点
解:∵M,N分别是边AB,AC的中点∴MN∥BC,MN=
| 1 |
| 2 |
又∵BD∥AC
∴∠DBA=∠A=60°
∵BM=AM,∠BMD=∠AMN
∴△BMD≌△AMN
∴DM=MN=1
连接OA交MN于点G,则OA⊥BC
∴OA⊥EF
∴EG=FG,MG=FN
由相交弦定理得:ME•MF=MA•MB
∴EM(EM+1)=1
解得EM=
| ||
| 2 |
-
| ||
| 2 |
∴DE=DM-EM=
3-
| ||
| 2 |
∴DE(3-DE)=1
解得DE=
3-
| ||
| 2 |
3+
| ||
| 2 |
点评:本题利用了三角形的中位线的性质,等边三角形的性质,全等三角形的判定和性质,一元二次方程的解法求解.

练习册系列答案
相关题目
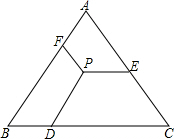 如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( )
如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( ) 31、如图,△ABC是等边三角形,AD是△ABC的角平分线,延长AC到E,使得CE=CD.
31、如图,△ABC是等边三角形,AD是△ABC的角平分线,延长AC到E,使得CE=CD.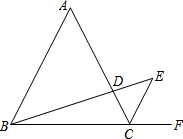 (2013•崇明县一模)如图,△ABC是等边三角形,且AD•ED=BD•CD.
(2013•崇明县一模)如图,△ABC是等边三角形,且AD•ED=BD•CD.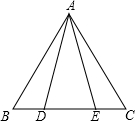 如图,△ABC是等边三角形,AD=AE,BE=CD.图中全等三角形有
如图,△ABC是等边三角形,AD=AE,BE=CD.图中全等三角形有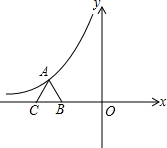 如图,△ABC是等边三角形,点A在反比例函数y=-
如图,△ABC是等边三角形,点A在反比例函数y=-