题目内容
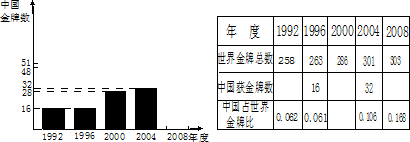
下表(或直方图)是25届到29届奥运会金牌总数与我国奥运健儿获得的金牌数的有关数据.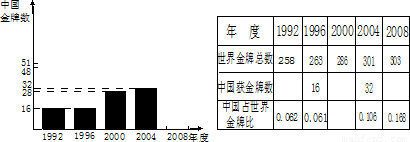
请根据图形的有关信息补全直方图,并把表格中的数据填写完整.
(1)1992至2008年中国获金牌数的极差是______.
(2)2008年第29届奥运会我国奥运健儿还获得银牌21枚、铜牌28枚的骄人成绩.体育总局提出到2016年第31届奥运会要获得奖牌总数达到121枚,假设后两届运动会奖牌数的增长率相同,求后两届奖牌数的增长率.
【答案】分析:(1)根据极差的定义,极差是指一组数据中最大数据与最小数据的差,结合数据即可得出1992至2008年中国获金牌数的极差.
(2)设这两年的年平均增长率为x%,则经过两次增长以后奖牌数100(1+x%)2枚,即可列方程求解,
解答:解:首先从直方图可得出1992年的金牌数为16枚,2000年的金牌数为28枚,有表格得出2000年的金牌比为: =0.098;2008年的金牌数为303×0.168=51;
=0.098;2008年的金牌数为303×0.168=51;
补充图形如下:
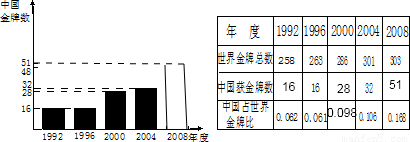
(1)1992至2008年中国获金牌数的极差=51-16=35枚;
(2)设这两年的年平均增长率为x%,则可得:100(1+x%)2=121,
解得:x=10%.
答:这两年的增长率为10%.
点评:本题考查了一元二次方程的应用及极差的概念,结合了直方图及图表的知识,有一定的综合性,解答本题的关键是具有根据图表获取信息的能力,也要掌握一元二次方程求增长率方程的列法.
(2)设这两年的年平均增长率为x%,则经过两次增长以后奖牌数100(1+x%)2枚,即可列方程求解,
解答:解:首先从直方图可得出1992年的金牌数为16枚,2000年的金牌数为28枚,有表格得出2000年的金牌比为:
 =0.098;2008年的金牌数为303×0.168=51;
=0.098;2008年的金牌数为303×0.168=51;补充图形如下:

(1)1992至2008年中国获金牌数的极差=51-16=35枚;
(2)设这两年的年平均增长率为x%,则可得:100(1+x%)2=121,
解得:x=10%.
答:这两年的增长率为10%.
点评:本题考查了一元二次方程的应用及极差的概念,结合了直方图及图表的知识,有一定的综合性,解答本题的关键是具有根据图表获取信息的能力,也要掌握一元二次方程求增长率方程的列法.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目