题目内容
【题目】如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的结论有 . 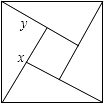
【答案】①②③
【解析】解:①∵△ABC为直角三角形, ∴根据勾股定理:x2+y2=AB2=49,
故本选项正确;
②由图可知,x﹣y=CE= ![]() =2,
=2,
故本选项正确;
③由图可知,四个直角三角形的面积与小正方形的面积之和为大正方形的面积,
列出等式为4× ![]() ×xy+4=49,
×xy+4=49,
即2xy+4=49;
故本选项正确;
④由2xy+4=49可得2xy=45①,
又∵x2+y2=49②,
∴①+②得,x2+2xy+y2=49+45,
整理得,(x+y)2=94,
x+y= ![]() ≠9,
≠9,
故本选项错误.
∴正确结论有①②③.
所以答案是①②③.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.

(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
平面图 | a | b | c | d |
顶点数(S) | 7 | |||
边数(M) | 9 | |||
区域数(N) | 3 |
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系为 ;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有 条边.

