题目内容
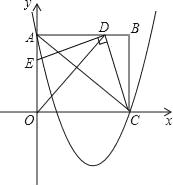
【题目】如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,C在x轴的正半轴上,已知A(0,8)、C(10,0),作∠AOC的平分线交AB于点D,连接CD,过点D作DE⊥CD交OA于点E.
(1)求点D的坐标;
(2)求证:△ADE≌△BCD;
(3)抛物线y=![]() x2﹣
x2﹣![]() x+8经过点A、C,连接AC.探索:若点P是x轴下方抛物线上一动点,过点P作平行于y轴的直线交AC于点M.是否存在点P,使线段MP的长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
x+8经过点A、C,连接AC.探索:若点P是x轴下方抛物线上一动点,过点P作平行于y轴的直线交AC于点M.是否存在点P,使线段MP的长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)(8,8);(2)详见解析;(3)存在,P点坐标为(5,﹣6).
【解析】
(1)利用角平分线的性质以及矩形的性质得出∠ADO=∠DOC,以及∠AOD=∠ADO,进而得出答案;
(2)利用全等三角形的判定方法(ASA)即可得出答案;
(3)设P点坐标为(t,![]() t2﹣
t2﹣![]() t+8),设AC所在的直线的函数关系式为y=kx+b,根据A(0,8)、C(10,0),求出AC的解析式,进而用t表示出PM的长,利用二次函数的性质求出PM的最值,点P的坐标也可以求出.
t+8),设AC所在的直线的函数关系式为y=kx+b,根据A(0,8)、C(10,0),求出AC的解析式,进而用t表示出PM的长,利用二次函数的性质求出PM的最值,点P的坐标也可以求出.
解:(1)∵OD平分∠AOC,∴∠AOD=∠DOC.
∵四边形AOCB是矩形,
∴AB∥OC
∴∠AOD=∠DOC
∴∠AOD=∠ADO.
∴OA=AD(等角对等边).
∵A点的坐标为(0,8),
∴D点的坐标为(8,8)
(2)∵四边形AOCB是矩形,
∴∠OAB=∠B=90°,BC=OA.
∵OA=AD,
∴AD=BC.
∵ED⊥DC
∴∠EDC=90°
∴∠ADE+∠BDC=90°
∴∠BDC+∠BCD=90°.
∴∠ADE=∠BCD.

在△ADE和△BCD中,
∵∠DAE=∠B,AD=BC,∠ADE=∠BCD,
∴△ADE≌△BCD(ASA)
(3)存在,
∵二次函数的解析式为:,点P是抛物线上的一动点,
∴设P点坐标为(t,![]() t2﹣
t2﹣![]() t+8)
t+8)
设AC所在的直线的函数关系式为y=kx+b,
∵A(0,8)、C(10,0),
∴![]() ,解得
,解得
∴直线AC的解析式y=-![]() .
.
∵PM∥y轴,
∴M(t,-![]() ).
).
∴PM=﹣( ![]() t2﹣
t2﹣![]() t+8)+(-
t+8)+(-![]() )=-
)=-![]() (t-5)2+10.
(t-5)2+10.
∴当t=5时,PM有最大值为10.
∴所求的P点坐标为(5,﹣6).

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案