题目内容
某社区要调查社区居民双休日的学习状况,采用下列调查方式: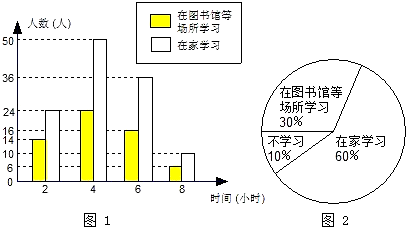
①从一幢高层住宅楼中选取200名居民;
②从不同住宅楼中随机选取200名居民;
③选取社区内200名在校学生.
(1)上述调查方式最合理的是
(2)将最合理的调查方式得到的数据制成扇形统计图(如图1)和频数分布直方图(如图2),在这个调查中,200名居民双休日在家学习的有
(3)请估计该社区2000名居民双休日学习时间不少于4小时的人数.
分析:(1)抽样调查为了获得较为准确的调查结果,抽样时要注意样本的代表性和广泛性;
(2)从扇形统计图中可以看出,双休日在家学习的人占60%;
(3)首先从图2中计算出双休日学习时间不少于4小时的居民占总体的百分比,然后就可以通过样本估计总体,算出该社区2 000名居民双休日学习时间不少于4小时的人数.
(2)从扇形统计图中可以看出,双休日在家学习的人占60%;
(3)首先从图2中计算出双休日学习时间不少于4小时的居民占总体的百分比,然后就可以通过样本估计总体,算出该社区2 000名居民双休日学习时间不少于4小时的人数.
解答:解:(1)调查方式②更具有代表性和广泛性;
故答案为:②;
(2)在家学习的所占的比例是60%,因而在家学习的人数是:200×60%=120(人);
故答案为:120;
(3)学习时间不少于4小时的频率是:
=0.71.
该社区2 000名居民双休日学习时间不少于4小时的人数是:2000×0.71=1420(人).
估计该社区2000名居民双休日学习时间不少于4小时的人数为1420人.
故答案为:②;
(2)在家学习的所占的比例是60%,因而在家学习的人数是:200×60%=120(人);
故答案为:120;
(3)学习时间不少于4小时的频率是:
| 24+50+16+36+6+10 |
| 200 |
该社区2 000名居民双休日学习时间不少于4小时的人数是:2000×0.71=1420(人).
估计该社区2000名居民双休日学习时间不少于4小时的人数为1420人.
点评:统计的思想就是用样本的信息来估计总体的信息,本题体现了统计思想,考查了用样本估计总体.除此之外,本题还考查扇形统计图及相关计算.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目