题目内容
 (2012•宜昌)如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为
(2012•宜昌)如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为 |
| AD |
(1)求证:OF∥BD;
(2)若
| FE |
| ED |
| 1 |
| 2 |
①求证:点F为线段OC的中点;
②求图中阴影部分(弓形)的面积.
分析:(1)由垂径定理可知OC⊥AD,由圆周角定理可知BD⊥AD,从而证明OF∥BD;
(2)①由OF∥BD可证△ECF∽△EBD,利用相似比证明BD=2CF,再证OF为△ABD的中位线,得出BD=2OF,即CF=OF,证明点F为线段OC的中点;
②根据S阴=S扇形AOC-S△AOC,求面积.
(2)①由OF∥BD可证△ECF∽△EBD,利用相似比证明BD=2CF,再证OF为△ABD的中位线,得出BD=2OF,即CF=OF,证明点F为线段OC的中点;
②根据S阴=S扇形AOC-S△AOC,求面积.
解答:(1)证明:∵OC为半径,点C为弧AD的中点,
∴OC⊥AD,
∵AB为直径,
∴∠BDA=90°,BD⊥AD,
∴∠AFO=∠D=90°,
∴OF∥BD;
(2)证明:①∵点O为AB的中点,点F为AD的中点,
∴OF=
BD,
∵FC∥BD,
∴∠FCE=∠DBE,
又∵∠FEC=∠DEB,
∴△ECF∽△EBD,
∴
=
=
,
∴FC=
BD,
∴FC=FO,即点F为线段OC的中点,
②解:∵FC=FO,OC⊥AD,
∴AC=AO,
又∵AO=CO,
∴△AOC为等边三角形,
∴S阴=
-
×
×6×6=6π-9
(cm2).
答:图中阴影部分(弓形)的面积为(6π-9
)cm2.
∴OC⊥AD,
∵AB为直径,
∴∠BDA=90°,BD⊥AD,
∴∠AFO=∠D=90°,
∴OF∥BD;
(2)证明:①∵点O为AB的中点,点F为AD的中点,
∴OF=
| 1 |
| 2 |
∵FC∥BD,
∴∠FCE=∠DBE,
又∵∠FEC=∠DEB,
∴△ECF∽△EBD,
∴
| FC |
| BD |
| FE |
| ED |
| 1 |
| 2 |
∴FC=
| 1 |
| 2 |
∴FC=FO,即点F为线段OC的中点,
②解:∵FC=FO,OC⊥AD,
∴AC=AO,
又∵AO=CO,
∴△AOC为等边三角形,
∴S阴=
| 60×π×62 |
| 360 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
答:图中阴影部分(弓形)的面积为(6π-9
| 3 |
点评:本题考查了相似三角形的判定与性质,等边三角形的判定与性质,垂径定理,圆周角定理,扇形面积的计算.关键是熟练掌握各知识点的联系及互相转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•宜昌)如图,数轴上表示数-2的相反数的点是( )
(2012•宜昌)如图,数轴上表示数-2的相反数的点是( )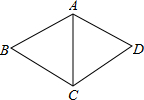 (2012•宜昌)如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( )
(2012•宜昌)如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( ) (2012•宜昌)如图,将三角尺与直尺贴在一起,使三角尺的直角顶点C(∠ACB=90°)在直尺的一边上,若∠1=
(2012•宜昌)如图,将三角尺与直尺贴在一起,使三角尺的直角顶点C(∠ACB=90°)在直尺的一边上,若∠1=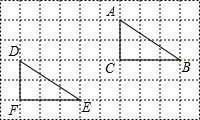 (2012•宜昌)如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
(2012•宜昌)如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )