题目内容
(2010•邯郸一模)在平面直角坐标中,Rt△OAB的两顶点A,B分别在y轴,x轴的正半轴上,点O是原点.其中点A(0,3),B(4,0),OC是Rt△OAB的高,点P以每秒1个单位长的速度在线段OB上由点O向点B运动(与端点不重合),过点P作PD⊥AP交AB于点D,设运动时间为t秒.(1)若△AOE的面积为
 ,求点E的坐标;
,求点E的坐标;(2)求证:△AOE∽△PBD;
(3)△PBD能否是等腰三角形?若能,求出此时t的值;若不能,请说明理由;
(4)当t=3时,直接写出此时
 的值.
的值.
【答案】分析:(1)过点E作EF⊥OA于F,则EF是△OAE的高,易知OA的长,根据△OAE的面积即可求得EF的值,易证得△OEF∽△BAO,根据相似三角形所得比例线段即可求得OE的长,也就能得到E点的坐标.
(2)由于AP⊥PD,那么∠DPB和∠EAO同为∠APO的余角,则∠EAO=∠DPB,易证得∠AOE=∠PBD,由此可证得所求的三角形相似.
(3)由于△APD中,∠APD=90°,故∠ADP是锐角,∠BDP是钝角,若△BPD是等腰三角形,那么∠BDP必为顶角,即DP=BD;由于△AOE∽△PBD,那么△AOE也是等腰三角形,即OE=AE,根据等腰三角形三线合一的性质知:AF=FO= ,仿照(1)的方法,可通过△OEF∽△BAO,求得EF的长,而△AEF∽△APO,根据相似三角形所得比例线段即可求得OP的长即t的值.
,仿照(1)的方法,可通过△OEF∽△BAO,求得EF的长,而△AEF∽△APO,根据相似三角形所得比例线段即可求得OP的长即t的值.
(4)当t=3时,OP=OA=3,则AP=3 ;由(2)证得△AOE∽△PBD,那么AE:PD=OA:PB,由于OA=3,PB=OB-OP=1,因此AE=3PD,可设PD=x,则AE=3x,易得△AEC∽△ADP,则有:
;由(2)证得△AOE∽△PBD,那么AE:PD=OA:PB,由于OA=3,PB=OB-OP=1,因此AE=3PD,可设PD=x,则AE=3x,易得△AEC∽△ADP,则有: ,根据射影定理可在Rt△ABO中求出AC的长,利用勾股定理可求得EC的表达式,将它们代入上式比例式中,即可求得x的值,进而可得到EC、AE的长,有了AE、AP的长,即可得到AE:EP的值.
,根据射影定理可在Rt△ABO中求出AC的长,利用勾股定理可求得EC的表达式,将它们代入上式比例式中,即可求得x的值,进而可得到EC、AE的长,有了AE、AP的长,即可得到AE:EP的值.
解答:(1)解:过点E作EF⊥OA于点F,
∵△AOE的面积为 ,OA=3,
,OA=3,
∴EF=1;
∵∠EOF=∠ABO=90°-∠BOC,
∠EFO=∠AOB=90°,
∴△OEF∽△BAO,
 ,即
,即 ,所以OF=
,所以OF= ,
,
∴点E的坐标为(1, ).
).
(2)证明:∵Rt△OAB中,OC为斜边AB边上的高,
∴∠EOA+∠OAC=90°,∠DBP+∠OAC=90°,
∴∠EOA=∠DBP,
∴∠EOA=∠DBP=90°-∠BOC,
 ∠AEO=∠PDB=90°+∠PAB,
∠AEO=∠PDB=90°+∠PAB,
∴△AOE∽△PBD.
(3)△PBD可以是等腰三角形,
∵∠PDB=90°+∠PAB>90°,
∴如果△PBD是等腰三角形,∠PDB只能顶角,即DP=DB,
当△PDB是等腰三角形,∵△AOE∽△PBD,
∴△AOE是等腰三角形,且EA=EO;
过点E作EF⊥AO于点F,则AF=OF= ;
;
∵△OEF∽△BAO,
∴ ,即
,即 ,所以EF=
,所以EF= ,
,
∵△AFE∽△AOP,
∴ ,即
,即 ,所以t=
,所以t= ,
,
∴当△PBD是等腰三角形时,t= ;
;
(4)当t=3时, .
.
点评:此题主要考查的是相似三角形的性质以及等腰三角形的判定;在解答过程中,反复多次用到了相似三角形的性质,能够将所求线段和已知线段用相似三角形串联起来是解答此题的关键.
(2)由于AP⊥PD,那么∠DPB和∠EAO同为∠APO的余角,则∠EAO=∠DPB,易证得∠AOE=∠PBD,由此可证得所求的三角形相似.
(3)由于△APD中,∠APD=90°,故∠ADP是锐角,∠BDP是钝角,若△BPD是等腰三角形,那么∠BDP必为顶角,即DP=BD;由于△AOE∽△PBD,那么△AOE也是等腰三角形,即OE=AE,根据等腰三角形三线合一的性质知:AF=FO=
 ,仿照(1)的方法,可通过△OEF∽△BAO,求得EF的长,而△AEF∽△APO,根据相似三角形所得比例线段即可求得OP的长即t的值.
,仿照(1)的方法,可通过△OEF∽△BAO,求得EF的长,而△AEF∽△APO,根据相似三角形所得比例线段即可求得OP的长即t的值.(4)当t=3时,OP=OA=3,则AP=3
 ;由(2)证得△AOE∽△PBD,那么AE:PD=OA:PB,由于OA=3,PB=OB-OP=1,因此AE=3PD,可设PD=x,则AE=3x,易得△AEC∽△ADP,则有:
;由(2)证得△AOE∽△PBD,那么AE:PD=OA:PB,由于OA=3,PB=OB-OP=1,因此AE=3PD,可设PD=x,则AE=3x,易得△AEC∽△ADP,则有: ,根据射影定理可在Rt△ABO中求出AC的长,利用勾股定理可求得EC的表达式,将它们代入上式比例式中,即可求得x的值,进而可得到EC、AE的长,有了AE、AP的长,即可得到AE:EP的值.
,根据射影定理可在Rt△ABO中求出AC的长,利用勾股定理可求得EC的表达式,将它们代入上式比例式中,即可求得x的值,进而可得到EC、AE的长,有了AE、AP的长,即可得到AE:EP的值.解答:(1)解:过点E作EF⊥OA于点F,
∵△AOE的面积为
 ,OA=3,
,OA=3,∴EF=1;
∵∠EOF=∠ABO=90°-∠BOC,
∠EFO=∠AOB=90°,
∴△OEF∽△BAO,
 ,即
,即 ,所以OF=
,所以OF= ,
,∴点E的坐标为(1,
 ).
).(2)证明:∵Rt△OAB中,OC为斜边AB边上的高,
∴∠EOA+∠OAC=90°,∠DBP+∠OAC=90°,
∴∠EOA=∠DBP,
∴∠EOA=∠DBP=90°-∠BOC,
 ∠AEO=∠PDB=90°+∠PAB,
∠AEO=∠PDB=90°+∠PAB,∴△AOE∽△PBD.
(3)△PBD可以是等腰三角形,
∵∠PDB=90°+∠PAB>90°,
∴如果△PBD是等腰三角形,∠PDB只能顶角,即DP=DB,
当△PDB是等腰三角形,∵△AOE∽△PBD,
∴△AOE是等腰三角形,且EA=EO;
过点E作EF⊥AO于点F,则AF=OF=
 ;
;∵△OEF∽△BAO,
∴
 ,即
,即 ,所以EF=
,所以EF= ,
,∵△AFE∽△AOP,
∴
 ,即
,即 ,所以t=
,所以t= ,
,∴当△PBD是等腰三角形时,t=
 ;
;(4)当t=3时,
 .
.点评:此题主要考查的是相似三角形的性质以及等腰三角形的判定;在解答过程中,反复多次用到了相似三角形的性质,能够将所求线段和已知线段用相似三角形串联起来是解答此题的关键.

练习册系列答案
相关题目


 +1=c
+1=c
 (其中k是使
(其中k是使 为奇数的正整数),并且运算重复进行.例如:取n=26,则:
为奇数的正整数),并且运算重复进行.例如:取n=26,则: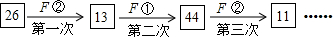 若n=15,则第15次“F”运算的结果是( )
若n=15,则第15次“F”运算的结果是( )