题目内容
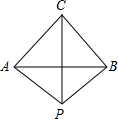如图，已知AC=BC，PC⊥AB，连接PA和PB，则PA________PB．（填“＞”，“＜”，“=”）
=
分析：根据等腰三角形三线合一的性质可得PC垂直平分AB，再根据线段垂直平分线上的点到线段两端点的距离相等的性质解答．
解答：∵AC=BC，PC⊥AB，
∴PC垂直平分AB（等腰三角形三线合一），
∴PA=PB（线段垂直平分线上的点到线段两端点的距离相等）．
故答案为：=．
点评：本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，等腰三角形三线合一的性质，判断出PC垂直平分AB是解题的关键．
分析：根据等腰三角形三线合一的性质可得PC垂直平分AB，再根据线段垂直平分线上的点到线段两端点的距离相等的性质解答．
解答：∵AC=BC，PC⊥AB，
∴PC垂直平分AB（等腰三角形三线合一），
∴PA=PB（线段垂直平分线上的点到线段两端点的距离相等）．
故答案为：=．
点评：本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，等腰三角形三线合一的性质，判断出PC垂直平分AB是解题的关键．
练习册系列答案
考前必练系列答案
相关题目
19、如图，已知AC⊥BC，CD⊥AB，DE⊥AC，∠1+∠2=180°，要证HF⊥AB，请完善证明过程，并在括号内填上相应依据：
（2012•肇庆）如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．
如图，已知AC=BC，∠1=∠2，点D、E分别在CA、CB的延长线上．
如图，已知AC⊥BC，CD⊥AB，DE⊥AC，∠1与∠2互补，判断HF与AB是否垂直，并说明理由．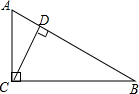
如图，已知AC⊥BC，CD⊥AB于点D，AC=5cm，BC=12cm，AB=13cm，那么点B到AC的距离是