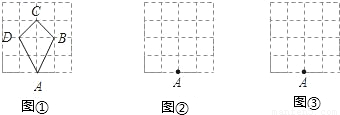
题目内容
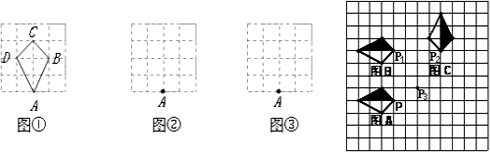
今有一机器人接到指令:在4×4的正方形(每个小正方形边长均为1)网格的格点上跳跃,每次跳跃的距离只能为1或 或2或
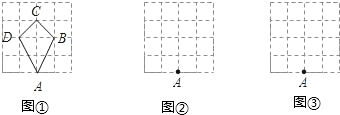
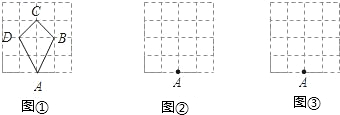
或2或 ,机器人从A点出发连续跳跃4次恰好跳回A点,且跳跃的路线(A→B→C→D→A)所成的封闭图形为多边形.例如图①机器人跳跃四次的路线图形是四边形ABCD.
,机器人从A点出发连续跳跃4次恰好跳回A点,且跳跃的路线(A→B→C→D→A)所成的封闭图形为多边形.例如图①机器人跳跃四次的路线图形是四边形ABCD.
仿照图①操作:(1)请你在网格图②中画出机器人跳跃的路线图形是直角梯形ABCD(只画一个图即可);
(2)请在网格图③中画出机器人跳跃的路线图形是面积为2的平行四边形ABCD(只画一个图即可).
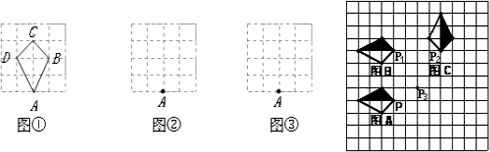
(3)在方格纸中,如图如何通过平移或旋转这两种变换,由图形A______得到图形B,再由图形B先______(怎样平移),再______(怎样旋转)得到图形C(对于平移变换要求回答出平移的方向和平移的距离;对于旋转变换要求回答出旋转中心、旋转方向和旋转角度);
(4)如图,如果点P、P3的坐标分别为(0,0)、(2,1),写出点P2的坐标是______;
(5)图形B能绕某点Q顺时针旋转90°得到图形C,则点Q的坐标是______;
(6)图形A能绕某点R顺时针旋转90°得到图形C,则点R的坐标是______.
注:方格纸中的小正方形的边长为1个单位长度.
解:(1)如图所示:
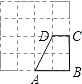
(2)如图所示:

(3)在方格纸中通过平移或旋转这两种变换,由图形A向上平移4个单位长度得到图形B;
再由图形B先先向右平移4个单位,再再绕点P2逆时针旋转90°得到图形C;
(4)∵如图,如果点P、P3的坐标分别为(0,0)、(2,1),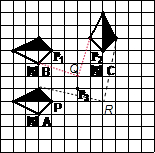
∴P2 (4,4);
(5)如图,∵图形B能绕某点Q顺时针旋转90°得到图形C,
则点Q的坐标是Q(2,2);
(6)如图,∵图形A能绕某点R顺时针旋转90°得到图形C,
则点R的坐标是R(4,0).
故答案为:上平移4个单位长度;B先先向右平移4个单位,再再绕点P2逆时针旋转90°;(4,4);(2,2);(4,0).
分析:(1)利用直角边为1,2的直角三角形的斜边等于 ,可构造边长分别为1,2,2,
,可构造边长分别为1,2,2, 的直角梯形;
的直角梯形;
(2)构造一边长为2,高为1的平行四边形即可.
(3)如图,根据方格纸中A和B的位置可以确定图形变换方式;然后根据B和C也可以确定图形变换方式;
(4)根据(1)和已知条件首先确定P、P3和P2的关系,然后就可以确定P2的坐标;
(5)由于图形B能绕某点Q顺时针旋转90°得到图形C,首先可以确定两组旋转对应点,然后根据旋转的性质即可确定旋转中心Q的坐标;
(6)由于图形A能绕某点R顺时针旋转90°得到图形C,首先可以确定两组旋转对应点的坐标,然后根据旋转的性质即可确定点R的坐标.
点评:此题主要考查了旋转、平移的性质、也考查了坐标与图形变换之间的关系,解题时首先利用平移、旋转的性质确定变换后的图形的位置,然后利用坐标与图形变换之间的关系确定坐标,以及勾股定理、平行四边形的面积来解决问题.

(2)如图所示:

(3)在方格纸中通过平移或旋转这两种变换,由图形A向上平移4个单位长度得到图形B;
再由图形B先先向右平移4个单位,再再绕点P2逆时针旋转90°得到图形C;
(4)∵如图,如果点P、P3的坐标分别为(0,0)、(2,1),

∴P2 (4,4);
(5)如图,∵图形B能绕某点Q顺时针旋转90°得到图形C,
则点Q的坐标是Q(2,2);
(6)如图,∵图形A能绕某点R顺时针旋转90°得到图形C,
则点R的坐标是R(4,0).
故答案为:上平移4个单位长度;B先先向右平移4个单位,再再绕点P2逆时针旋转90°;(4,4);(2,2);(4,0).
分析:(1)利用直角边为1,2的直角三角形的斜边等于
 ,可构造边长分别为1,2,2,
,可构造边长分别为1,2,2, 的直角梯形;
的直角梯形;(2)构造一边长为2,高为1的平行四边形即可.
(3)如图,根据方格纸中A和B的位置可以确定图形变换方式;然后根据B和C也可以确定图形变换方式;
(4)根据(1)和已知条件首先确定P、P3和P2的关系,然后就可以确定P2的坐标;
(5)由于图形B能绕某点Q顺时针旋转90°得到图形C,首先可以确定两组旋转对应点,然后根据旋转的性质即可确定旋转中心Q的坐标;
(6)由于图形A能绕某点R顺时针旋转90°得到图形C,首先可以确定两组旋转对应点的坐标,然后根据旋转的性质即可确定点R的坐标.
点评:此题主要考查了旋转、平移的性质、也考查了坐标与图形变换之间的关系,解题时首先利用平移、旋转的性质确定变换后的图形的位置,然后利用坐标与图形变换之间的关系确定坐标,以及勾股定理、平行四边形的面积来解决问题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
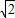 或2或
或2或 ,机器人从A点出发连续跳跃4次恰好跳回A点,且跳跃的路线(A?B?C?D?A)所成的封闭图形为多边形.例如图①机器人跳跃四次的路线图形是四边形ABCD.仿照图①操作:
,机器人从A点出发连续跳跃4次恰好跳回A点,且跳跃的路线(A?B?C?D?A)所成的封闭图形为多边形.例如图①机器人跳跃四次的路线图形是四边形ABCD.仿照图①操作: