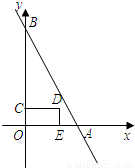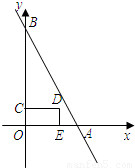题目内容
(2009•伊春)如图,抛物线y= x2+bx+c经过A(-
x2+bx+c经过A(-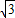 ,0)、B(0,-3)两点,此抛物线的对称轴为直线l,顶点为C,且l与直线AB交于点D.
,0)、B(0,-3)两点,此抛物线的对称轴为直线l,顶点为C,且l与直线AB交于点D.(1)求此抛物线的解析式;
(2)直接写出此抛物线的对称轴和顶点坐标;
(3)连接BC,求证:BC=CD.
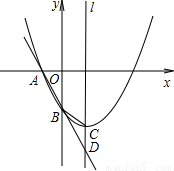
【答案】分析:(1)利用待定系数法,将点A,B的坐标代入解析式即可求得b,c的值,即可得解析式;
(2)利用公式:二次函数y=ax2+bx+c的对称轴为x=- ,顶点坐标为(-
,顶点坐标为(- ,
, )即可求解;
)即可求解;
(3)如图可知点B是抛物线与y轴的交点,即可求得BC的长,点D是直线AB与对称轴的交点,求得直线AB的解析式即可求得D的坐标,则可求得CD的长,则可证得结果.
解答:(1)解:∵抛物线y= x2+bx+c
x2+bx+c
经过A(- ,0)、B(0,-3)两点
,0)、B(0,-3)两点
∴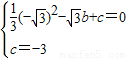
解得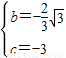
∴此抛物线的解析式为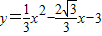 .
.
(2)解:由(1)可得此抛物线的对称轴l为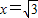 ,
,
顶点C的坐标为( ,-4).
,-4).
(3)证明:∵过A、B两点的直线解析式为
∴当 时,y=-6
时,y=-6
∴点D的纵坐标为-6
∴CD=|-6|-|-4|=2
作BE⊥l于点E,则
∴CE=4-3=1
由勾股定理得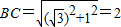
∴BC=DC.
点评:此题属于中考中的压轴题,难度较大,知识点考查的较多而且联系密切,需要学生认真审题.此题考查了二次函数与一次函数的综合知识,解题的关键是要注意数形结合思想的应用.
(2)利用公式:二次函数y=ax2+bx+c的对称轴为x=-
 ,顶点坐标为(-
,顶点坐标为(- ,
, )即可求解;
)即可求解;(3)如图可知点B是抛物线与y轴的交点,即可求得BC的长,点D是直线AB与对称轴的交点,求得直线AB的解析式即可求得D的坐标,则可求得CD的长,则可证得结果.
解答:(1)解:∵抛物线y=
 x2+bx+c
x2+bx+c经过A(-
 ,0)、B(0,-3)两点
,0)、B(0,-3)两点∴
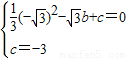
解得
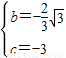
∴此抛物线的解析式为
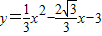 .
.(2)解:由(1)可得此抛物线的对称轴l为
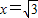 ,
,顶点C的坐标为(
 ,-4).
,-4).(3)证明:∵过A、B两点的直线解析式为

∴当
 时,y=-6
时,y=-6∴点D的纵坐标为-6
∴CD=|-6|-|-4|=2
作BE⊥l于点E,则

∴CE=4-3=1
由勾股定理得
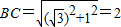
∴BC=DC.
点评:此题属于中考中的压轴题,难度较大,知识点考查的较多而且联系密切,需要学生认真审题.此题考查了二次函数与一次函数的综合知识,解题的关键是要注意数形结合思想的应用.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目