题目内容
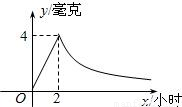
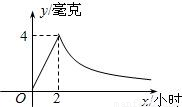
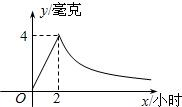 如图,病人按规定的剂量服用某药物,测得服药后2小时,每毫升血液中含药量达到最大值为4毫克.已知服药后,2小时前每毫升血液中含药量y(毫克)与时间x(小时)成正比例;2小时后y与x成反比例.
如图,病人按规定的剂量服用某药物,测得服药后2小时,每毫升血液中含药量达到最大值为4毫克.已知服药后,2小时前每毫升血液中含药量y(毫克)与时间x(小时)成正比例;2小时后y与x成反比例.(1)当0≤x≤2时;x>2时,分别求y与x的函数关系式?
(2)如果每毫升血液中含药量不低于2毫克时治疗有效,则那么服药一次,治疗疾病的有效时间是多长?
分析:(1)设正比例函数关系式为y=kx,反比例函数关系式为y=
,把(2,4)分别代入求k、m的值,确定函数关系式;
(2)把y=2分别代入两个函数关系式求时间,再求时间差.
| m |
| x |
(2)把y=2分别代入两个函数关系式求时间,再求时间差.
解答:解:(1)当0≤x≤2时;设y=kx
把(2,4)代入得:k=2,
∴y=2x,
当x>2时,设y=
,
把(2,4)代入得:m=8,
∴y=
;
(2)当y=2时;得
x1=1,x2=4,
∴有效时间=4-1=3小时.
答:治疗疾病的有效时间是3小时.
把(2,4)代入得:k=2,
∴y=2x,
当x>2时,设y=
| m |
| x |
把(2,4)代入得:m=8,
∴y=
| 8 |
| x |
(2)当y=2时;得
x1=1,x2=4,
∴有效时间=4-1=3小时.
答:治疗疾病的有效时间是3小时.
点评:本题考查了反比例函数的实际应用.关键是建立两个函数关系式,当函数值相等时,分别求出自变量的值并作差.

练习册系列答案
相关题目
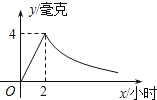 病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.
病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.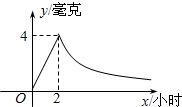 如图,病人按规定的剂量服用某药物,测得服药后2小时,每毫升血液中含药量达到最大值为4毫克.已知服药后,2小时前每毫升血液中含药量y(毫克)与时间x(小时)成正比例;2小时后y与x成反比例.
如图,病人按规定的剂量服用某药物,测得服药后2小时,每毫升血液中含药量达到最大值为4毫克.已知服药后,2小时前每毫升血液中含药量y(毫克)与时间x(小时)成正比例;2小时后y与x成反比例.