题目内容
已知:抛物线与直线y=x+3分别交于x轴和y轴上同一点,交点分别是点A和点C,且抛物线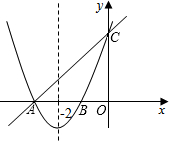 的对称轴为直线x=-2.
的对称轴为直线x=-2.(1)求出抛物线与x轴的两个交点A、B的坐标.
(2)试确定抛物线的解析式.
(3)观察图象,请直接写出二次函数值小于一次函数值的自变量x的取值范围.
分析:(1)根据已知得出点A、C的坐标,再利用点A与点B关于直线x=-2对称,即可求出B点坐标;
(2)利用待定系数法求二次函数解析式,即可得出答案;
(3)由图象观察可知,二次函数值小于一次函数值时,得出x的取值范围.
(2)利用待定系数法求二次函数解析式,即可得出答案;
(3)由图象观察可知,二次函数值小于一次函数值时,得出x的取值范围.
解答:解:(1)y=x+3中,
当y=0时,x=-3,
∴点A的坐标为(-3,0)(1分),
当x=0时,y=3,
∴点C坐标为(0,3),
∵抛物线的对称轴为直线x=-2,
∴点A与点B关于直线x=-2对称,
∴点B的坐标是(-1,0)(1分);
(2)设二次函数的解析式为y=ax2+bx+c,
∵二次函数的图象经过点C(0,3)和点A(-3,0),且对称轴是直线x=-2,
∴可列得方程组:
(1分),
解得:
,
∴二次函数的解析式为y=x2+4x+3(1分),
(或将点A、点B、点C的坐标依次代入解析式中求出a、b、c的值也可);
(3)由图象观察可知,当-3<x<0时,二次函数值小于一次函数值(2分).
当y=0时,x=-3,
∴点A的坐标为(-3,0)(1分),
当x=0时,y=3,
∴点C坐标为(0,3),
∵抛物线的对称轴为直线x=-2,
∴点A与点B关于直线x=-2对称,
∴点B的坐标是(-1,0)(1分);
(2)设二次函数的解析式为y=ax2+bx+c,
∵二次函数的图象经过点C(0,3)和点A(-3,0),且对称轴是直线x=-2,
∴可列得方程组:
|
解得:
|
∴二次函数的解析式为y=x2+4x+3(1分),
(或将点A、点B、点C的坐标依次代入解析式中求出a、b、c的值也可);
(3)由图象观察可知,当-3<x<0时,二次函数值小于一次函数值(2分).
点评:此题主要考查了一次函数与交点坐标求法以及待定系数法求二次函数解析式和结合图象比较函数大小关系等知识,利用函数图象比较函数的大小关系是难点,同学们应重点掌握.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目


