题目内容
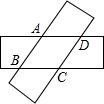 如图,剪两张对边平行的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )
如图,剪两张对边平行的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )| A、∠ABC=∠ADC,∠BAD=∠BCD | B、AB=BC | C、AB=CD,AD=BC | D、∠DAB+∠BCD=180° |
分析:首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的等积转换可得邻边相等,则四边形ABCD为菱形.所以根据菱形的性质进行判断.
解答: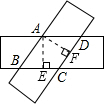 解∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,
解∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形(对边相互平行的四边形是平行四边形);
过点D分别作AB,BC边上的高为AE,AF.则
AE=AF(两纸条相同,纸条宽度相同);
∵平行四边形ABCD中,S△ABD=S△DBC,即AB×DE=BC×DF,
∴AB=BC.故B正确;
∴平行四边形ABCD为菱形(邻边相等的平行四边形是菱形).
∴∠ABC=∠ADC,∠BAD=∠BCD(菱形的对角相等),故A正确;
AB=CD,AD=BC(平行四边形的对边相等),故C正确;
如果四边形ABCD是矩形时,该等式成立.故D不一定正确.
故选:D.
 解∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,
解∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形(对边相互平行的四边形是平行四边形);
过点D分别作AB,BC边上的高为AE,AF.则
AE=AF(两纸条相同,纸条宽度相同);
∵平行四边形ABCD中,S△ABD=S△DBC,即AB×DE=BC×DF,
∴AB=BC.故B正确;
∴平行四边形ABCD为菱形(邻边相等的平行四边形是菱形).
∴∠ABC=∠ADC,∠BAD=∠BCD(菱形的对角相等),故A正确;
AB=CD,AD=BC(平行四边形的对边相等),故C正确;
如果四边形ABCD是矩形时,该等式成立.故D不一定正确.
故选:D.
点评:本题考查了菱形的判定与性质.注意:“邻边相等的平行四边形是菱形”,而非“邻边相等的四边形是菱形”.

练习册系列答案
相关题目
 4、将一张四边形纸片沿两组对边的中点连线剪开,得到四张小纸片,如图所示.用这四张小纸片一定可以拼成( )
4、将一张四边形纸片沿两组对边的中点连线剪开,得到四张小纸片,如图所示.用这四张小纸片一定可以拼成( )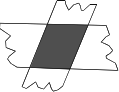
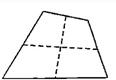 将一张四边形纸片沿两组对边的中点连线剪开,得到四张小纸片,如图所示.用这四张小纸片一定可以拼成
将一张四边形纸片沿两组对边的中点连线剪开,得到四张小纸片,如图所示.用这四张小纸片一定可以拼成