题目内容
（2001•呼和浩特）若tanα+cotα=3，α为锐角，则tan2α+cot2α= ．
【答案】分析：根据tanα•cotα=1并将tanα+cotα=3两边平方可得tan2α+cot2α的值．
解答：解：∵tanα•cotα=1，tanα+cotα=3，
∴（tanα+cotα）2=9，
即tan2α+cot2α+2tanα•cotα=9，
∴tan2α+cot2α+2=9，
∴tan2α+cot2α=7．
点评：本题考查了对同角的三角函数的关系：tanα•cotα=1应用．
解答：解：∵tanα•cotα=1，tanα+cotα=3，
∴（tanα+cotα）2=9，
即tan2α+cot2α+2tanα•cotα=9，
∴tan2α+cot2α+2=9，
∴tan2α+cot2α=7．
点评：本题考查了对同角的三角函数的关系：tanα•cotα=1应用．
练习册系列答案
名校课堂系列答案
相关题目
的图象经过点（1，-1），则函数y=kx-2的图象不经过第（ ）象限．
的图象经过点（1，-1），则函数y=kx-2的图象不经过第（ ）象限．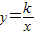
的图象经过点（1，-1），则函数y=kx-2的图象不经过第（ ）象限．