题目内容

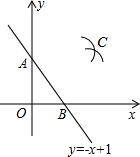如图，直线与坐标轴交于A、B两点，分别以点A、B为圆心，大于
1
2
AB长为半径作弧，两弧交于点C，若点C的坐标为（m+1，2n），则m与n的关系是（　　）
A、m+2n=1
B、m+2n=-1
C、m-2n=-1
D、2m-n=-1
练习册系列答案
相关题目
下列a与b成正比例的式子是（　　）
A、a2=bB、a=bC、a=4b+5D、以上都不对
一次函数y=-x+1的图象经过（　　）
A、一、二、三象限B、一、二、四象限C、一、三、四象限D、二、三、四象限
如图，A点的坐标为（-4，0），直线y=
3
x+n与坐标轴交于点B，C，连接AC，如果∠ACD=90°，则n的值为（　　）
A、-2
B、-
4
2
3
C、-
4
3
3
D、-
4
5
3
直线y=x-2与y轴的交点坐标是（　　）
A、（2，0）B、（-2，0）C、（0，2）D、（0，-2）
在直角坐标系中，一直线a向下平移3个单位后所得直线b经过点A（0，3），将直线b绕点A顺时针旋转60°后所得直线经过点B（-
3
，0），则直线a的函数关系式为（　　）
A、y=-
3
x
B、y=-
3
3
x
C、y=-
3
x+6
D、y=-
3
3
x+6
在平面直角坐标系中，将直线y=-2x+1的图象向左平移2个单位，再向上平移一个单位，得到的直线的解析式是（　　）
A、y=-2x-2B、y=-2x+6C、y=-2x-4D、y=-2x+4
某通讯公司提供了两种移动电话收费方式：方式1，收月基本费20元，再以每分钟0.1元的价格按通话时间计费；方式2，收月基本费20元，送80分钟通话时间，超过80分钟的部分，以每分钟0.15元的价格计费．
下列结论：
①如图描述的是方式1的收费方法；
②若月通话时间少于240分钟，选择方式2省钱；
③若月通讯费为50元，则方式1比方式2的通话时间多；
④若方式1比方式2的通讯费多10元，则方式1比方式2的通话时间多100分钟．
其中正确的是（　　）
A、只有①②B、只有③④C、只有①②③D、①②③④
下列计算正确的是（　　）
A、a2•a3=a6B、2a+3a=6aC、a2+a2+a2=3a2D、a2+a2+a2=a6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网