题目内容
已知关于x的方程 有实数根,则实数k的取值范围是______
有实数根,则实数k的取值范围是______
 有实数根,则实数k的取值范围是______
有实数根,则实数k的取值范围是______ 且k≠
且k≠ .
.二次方程有实数根即根的判别式△≥0,找出a,b,c的值代入列出k的不等式,求其取值范围.
解:因为关于x的二次方程(1-2k)x2-2 x-1=0有实数根,
x-1=0有实数根,
所以△=b2-4ac=(-2 )2-4(1-2k)×(-1)=4-4k≥0,
)2-4(1-2k)×(-1)=4-4k≥0,
解之得,k≤1.
又因为k≥0,1-2k≠0,即k≠ ,
,
所以k的取值范围是0≤k≤1且k≠ .
.
本题考查了一元二次方程根的判别式的应用.切记不要忽略一元二次方程二次项系数不为零和被开方数大于零这两个隐含条件.总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
解:因为关于x的二次方程(1-2k)x2-2
 x-1=0有实数根,
x-1=0有实数根,所以△=b2-4ac=(-2
 )2-4(1-2k)×(-1)=4-4k≥0,
)2-4(1-2k)×(-1)=4-4k≥0,解之得,k≤1.
又因为k≥0,1-2k≠0,即k≠
 ,
,所以k的取值范围是0≤k≤1且k≠
 .
.本题考查了一元二次方程根的判别式的应用.切记不要忽略一元二次方程二次项系数不为零和被开方数大于零这两个隐含条件.总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目

 +
+ x-4=0.
x-4=0. 的两根为
的两根为 ,
, ,则
,则 _____
_____ -2x-l=0
-2x-l=0
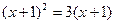

 ②
②