题目内容
| (23-1)(33-1)(43-1)…(1003-1) |
| (23+1)(33+1)(43+1)…(1003+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:首先根据n3-1=(n-1)(n2+n+1)和(n+1)3+1=(n+1+1)[(n+1)2-(n+1)+1]=(n+2)(n2+n+1),求出n3-1和(n+1)3+1的比,然后进行化简求出答案.
解答:解:∵n3-1=(n-1)(n2+n+1),
(n+1)3+1=(n+1+1)[(n+1)2-(n+1)+1],
=(n+2)(n2+n+1),
∴
=
=
(n≥2),
∴
,
=
,
=
,
=
≈
.
故选B.
(n+1)3+1=(n+1+1)[(n+1)2-(n+1)+1],
=(n+2)(n2+n+1),
∴
| (n3-1) |
| [(n+1)3+1] |
| [(n-1)(n2+n+1)] |
| [(n+2)(n2+n+1)] |
| n-1 |
| n+2 |
∴
| (23-1)(33-1)(43-1)…(1003-1) |
| (23+1)(33+1)(43+1)…(1003+1) |
=
| 1×2×3…×99×(1002+100+1) |
| 9×4×…×102 |
=
| 1×2×3…×99×(1002+100+1) |
| 9×4×…×100×101 |
=
| 1×2×3×(1002+100+1) |
| 9×100×101 |
| 2 |
| 3 |
故选B.
点评:本题主要考查立方公式的知识点,解答本题的关键是求出n3-1和(n+1)3+1的比,本题难度较大.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

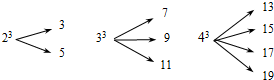 8、23,33和43分别可以按如图所示方式“分裂”成2个、3个和4个连续奇数的和.83也能按此规律进行“分裂”,则83“分裂”出的奇数中最大的是( )
8、23,33和43分别可以按如图所示方式“分裂”成2个、3个和4个连续奇数的和.83也能按此规律进行“分裂”,则83“分裂”出的奇数中最大的是( )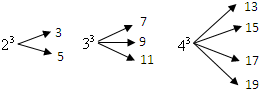 (2012•菏泽)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”,
(2012•菏泽)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”,