题目内容
如图,函数y=-| 1 | 2 |
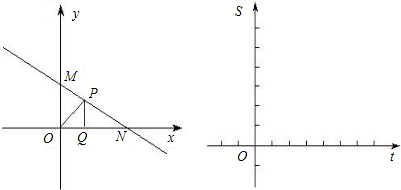
(1)试求S与t之间的函数关系式;
(2)在如图所示的直角坐标系内画出这个函数的图象,并利用图象求使得S=a(a>0)的点P的个数.
分析:本题要根据题意把各种情况都讨论出来,同时把△POQ的面积表示出来.(2)要根据题意列式整理分析,在根据解析式画出图象.
解答: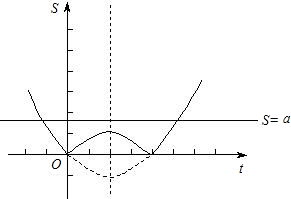 解:
解:
解法1:(1)①当t<0时,OQ=-t,PQ=-
t+2,
∴S=
•(-t)(-
t+2)=
t2-t;
②当0<t<4时,OQ=t,PQ=-
t+2,
∴S=
•t(-
t+2)=-
t2+t;
③当t>4时,OQ=t,PQ=-(-
t+2)=
t-2,
∴S=
•t(
t-2)=
t2-t;
④当t=0或4时,S=0;
于是,S=
(6分);
(2)S=
下图中的实线部分就是所画的函数图象.(12分)
观察图象可知:
当0<a<1时,符合条件的点P有四个;
当a=1时,符合条件的点P有三个;
当a>1时,符合条件的点P只有两个.(15分)
解法2:(1)∵OQ=|t|,PQ=|-
t+2|=|
t-2|,
∴S=
|t|•|
t-2|=
|t2-4t|(4分)
(2)S=
|t2-4t|=
(6分)
以下同解法1.
 解:
解:解法1:(1)①当t<0时,OQ=-t,PQ=-
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
②当0<t<4时,OQ=t,PQ=-
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
③当t>4时,OQ=t,PQ=-(-
| 1 |
| 2 |
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
④当t=0或4时,S=0;
于是,S=
|
(2)S=
|
下图中的实线部分就是所画的函数图象.(12分)
观察图象可知:
当0<a<1时,符合条件的点P有四个;
当a=1时,符合条件的点P有三个;
当a>1时,符合条件的点P只有两个.(15分)
解法2:(1)∵OQ=|t|,PQ=|-
| 1 |
| 2 |
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)S=
| 1 |
| 4 |
|
以下同解法1.
点评:本题考查一次函数有关分情况讨论的问题,解题中要注意对各种情况做出准确分析,尤其是t值做好取值范围的分段,

练习册系列答案
相关题目
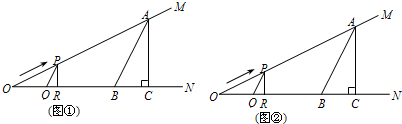
 已知二次函数y=4x2-4x-3的图象如图所示,
已知二次函数y=4x2-4x-3的图象如图所示,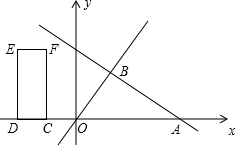
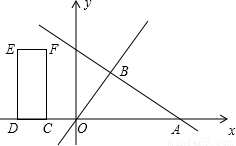
 x的图象于点B.矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴上方,DC=2,DE=4.当点C坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
x的图象于点B.矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴上方,DC=2,DE=4.当点C坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.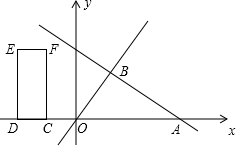
 x的图象于点B.矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴上方,DC=2,DE=4.当点C坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
x的图象于点B.矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴上方,DC=2,DE=4.当点C坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.