题目内容
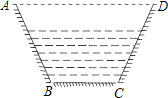 如图是一个等腰梯形状的水渠的横切面图,已知渠道底宽BC=2米,渠底与渠腰的夹角∠BCD=120°,渠腰CD=5米,求水渠的上口AD的长.
如图是一个等腰梯形状的水渠的横切面图,已知渠道底宽BC=2米,渠底与渠腰的夹角∠BCD=120°,渠腰CD=5米,求水渠的上口AD的长.
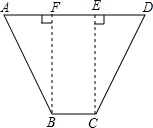 解:过C和B分别作CE⊥AD,BF⊥AD
解:过C和B分别作CE⊥AD,BF⊥AD∵∠BCD=120°
∴∠ECD=30°
∴ED=
 CD=
CD= ×5=2.5
×5=2.5∴四边形ABCD为等腰梯形,
∴
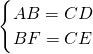
∴△AFB≌△DEC,
∴AF=ED=2.5
∵EF=BC=2
∴AD=DE+EF+FA=2.5+2+2.5=7(米)
分析:可以过C和B分别作CE⊥AD,BF⊥AD,则AF=DE,本题就可以转化为求DE的问题.
点评:等腰梯形的问题可以通过作高线转化为直角三角形的问题来解决.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
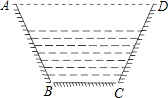 如图是一个等腰梯形状的水渠的横切面图,已知渠道底宽BC=2米,渠底与渠腰的夹角∠BCD=120°,渠腰CD=5米,求水渠的上口AD的长.
如图是一个等腰梯形状的水渠的横切面图,已知渠道底宽BC=2米,渠底与渠腰的夹角∠BCD=120°,渠腰CD=5米,求水渠的上口AD的长.

