题目内容
求证：对于任何实数x，代数式2x2+4x+3的值总大于0．
【答案】分析：将代数式前两项提取2，配方后根据完全平方式为非负数，得到代数式大于等于1，即对于任何实数x，代数式2x2+4x+3的值总大于0，得证．
解答：证明：∵对于任何实数x，（x+1）2≥0，
∴x2+4x+3=2（x2+2x）+3=2（x2+2x+1）+1=2（x+1）2+1≥1＞0，
则对于任何实数x，代数式2x2+4x+3的值总大于0．
点评：此题考查了配方法的应用，以及非负数的性质：偶次幂，灵活应用完全平方公式是解本题的关键．
解答：证明：∵对于任何实数x，（x+1）2≥0，
∴x2+4x+3=2（x2+2x）+3=2（x2+2x+1）+1=2（x+1）2+1≥1＞0，
则对于任何实数x，代数式2x2+4x+3的值总大于0．
点评：此题考查了配方法的应用，以及非负数的性质：偶次幂，灵活应用完全平方公式是解本题的关键．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
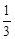)2≥0，
＞0
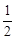)2≥0，
＞0