Question

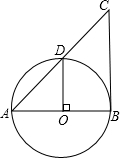如图，AB是⊙O的直径，CB切⊙O于B，连接AC交⊙O于D，若BC=8cm，DO⊥AB，求⊙O的半径．

Answer 1

分析：由AB是⊙O的直径，CB切⊙O于B，根据切线的性质，可得BC⊥AB，又由DO⊥AB，可得OD∥BC，即可证得△AOD∽△ABC，又由BC=8cm，即可求得⊙O的半径．

解答：解：∵AB是⊙O的直径，CB切⊙O于B，
∴BC⊥AB，
∵DO⊥AB，
∴OD∥BC，
∴△AOD∽△ABC，
∴OD：BC=OA：AB=1：2，
∵BC=8cm，
∴OD=4cm，
即⊙O的半径为4cm．

点评：此题考查了切线的性质以及相似三角形的判定与性质．此题比较简单，注意掌握数形结合思想的应用．