题目内容
【题目】已知,在□ABCD中,连接对角线![]() ,
, ![]() 平分线
平分线![]() 交
交![]() 于点
于点![]() ,
, ![]() 平分线
平分线![]() 交
交![]() 于点
于点![]() ,
, ![]() 、
、![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 上一点,且
上一点,且![]() 。
。
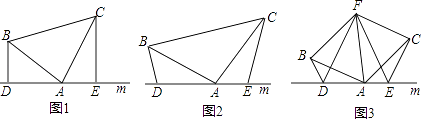
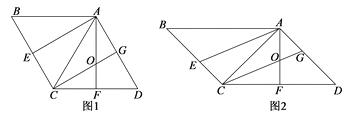
(1)如图1,若![]() 是等边三角形,
是等边三角形, ![]() ,求□ABCD的面积;
,求□ABCD的面积;
(2)如图2,若![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,求证:
,求证: ![]() 。
。
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据平行四边形ABCD的面积=2×SΔACD,求出ΔACD的面积即可;
(2)如图2中,延长OF到M,使得FM=OF,连接CM.只要证明AC=AM,OA=AG=CE即可解决问题.
试题解析:(1)如图1中,
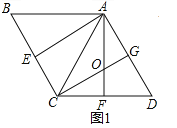
∵△ACD是等边三角形,
∴AC=CD=AD,∠ACD=∠D=∠CAD=60°,
∵∠OAC=∠OCA=30°,
∴OA=OC=2,
∵CG平分∠ACD,
∴CG⊥AD,
在RtΔAOG中,∵∠OAG=30°OA=2,
∴OG=![]() OA=1,AG=
OA=1,AG= ![]() ,
,
∴AD=2AG=2![]() ,
,
∴S△ACD=![]() ADCG=
ADCG=![]() =3
=3![]() .
.
∴平行四边形ABCD的面积=2S△ACD=6![]() .
.
(2)如图2中,延长OF到M,使得FM=OF,连接CM.
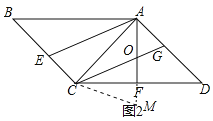
∵△ACD是等腰直角三角形,AF、CG是角平分线,
∴AF⊥CF,∠OAC=∠D=∠ACD=45°,∠OCA=∠DCG=22.5°,
∴∠OCF=∠OAC+∠OCA=67.5°,∠AGD=∠D+∠GCD=67.5°,
∴∠AOG=∠AGO,
∴OA=AG,
∵CF⊥OM,OF=OM,
∴CO=CM,
∴∠M=∠COM=67.5°,
∴∠ACM=180°﹣∠CAM﹣∠M=67.5°,
∴∠CAM=∠M,
∴CA=AM,
∵∠BAE=∠GCD=22.°5,AB∥CD,
∴∠BAC=∠ACD=45°,
∴∠EAC=∠ACG=22.5°,
∴AE∥CG,∵EC∥AG,
∴四边形AECG是平行四边形,
∴CE=AG=OA,
∴AC=AM=OA+OM=CE+2OF.