题目内容
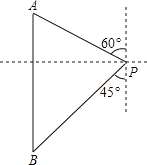
如图,某测量船位于海岛P的北偏西60°方向,距离海岛200海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的西南方向上的B处.求测量船从A处航行到B处的路程(结果保留根号).
练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
题目内容
如图,某测量船位于海岛P的北偏西60°方向,距离海岛200海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的西南方向上的B处.求测量船从A处航行到B处的路程(结果保留根号).

 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案