Question

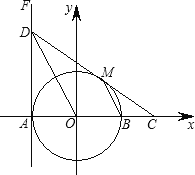
【题目】如图，在平面直角坐标系xOy中，⊙O交x轴于A、B两点，直线FA⊥x 轴于点A，点D在FA上，且DO平行⊙O的弦MB，连DM并延长交x轴于点C．

（1）判断直线DC与⊙O的位置关系，并给出证明；

（2）设点D的坐标为（﹣2，4），试求MC的长及直线DC的解析式．

Answer 1

【答案】见解析

【解析】试题分析：根据全等三角形、相似三角形的判断与性质以及一次函数的应用，利用全等三角形和相似三角形来得出线段相等或成比例解决本题．

（1）直线与圆的关系无非是相切，相交和相离，只要连接OM证明OM是否与DC垂直即可得出结论．

解题思路：通过证明三角形AOD和DOM全等来求解．已知的条件有OA=OM，一条公共边OD，只要证明出两组对应边的夹角相等即可．可通过OD∥MB，OM=OB来证得．

（2）求MC的长就要求出DC的长，也就是要求出AC的长．已知了D的坐标，那么AD，OA，AB的长就都知道了．

不难得出三角形OMC和DAC相似，因此可得出OM，AD，CM，AC的比例关系．已知了AD，OM的长，就能求出MC，AC的比例关系了．

在直角三角形ADC中，AD的长已知，DC=DM+MC=DA+MC，那么可根据勾股定理和MC，AC的比例关系求出MC的长．也就求出了M的坐标．有了M和D的坐标可以用待定系数法求出DC所在直线的函数解析式．

解：（1）答：直线DC与⊙O相切于点M．

证明如下：连OM，∵DO∥MB，

∴∠1=∠2，∠3=∠4．

∵OB=OM，

∴∠1=∠3．

∴∠2=∠4．

在△DAO与△DMO中， ．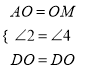

∴△DAO≌△DMO．

∴∠OMD=∠OAD．

由于FA⊥x轴于点A，

∴∠OAD=90°．

∴∠OMD=90°．即OM⊥DC．

∴DC切⊙O于M．

（2）由D（-2，4）知OA=2（即⊙O的半径），AD=4．

由（1）知DM=AD=4，由△OMC∽△DAC，知．

∴AC=2MC，

在Rt△ACD中，CD=MC+4．

由勾股定理，有（2MC）2+42=（MC+4）2，解得MC=或MC=0（不合题意，舍去）．

∴MC的长为．

∴点C（，0）．

设直线DC的解析式为y=kx+b．

则有．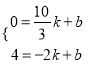

解得．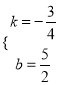

∴直线DC的解析式为y=-x+．