题目内容
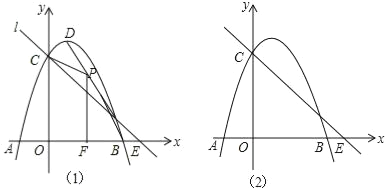
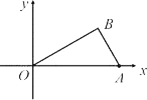
【题目】如图,已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
(1) 求点B的坐标;
(2) 若二次函数y=ax2+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
(3) 在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由.
【答案】
【1】(![]() )
)
【2】y=![]() x2+
x2+![]() x.
x.
【3】(![]() ),
),![]()
【解析】
(1) 在Rt△OAB中,∵∠AOB=30°,∴ OB=![]() . 过点B作BD垂直于x轴,垂足为D,则 OD=
. 过点B作BD垂直于x轴,垂足为D,则 OD=![]() ,BD=
,BD=![]() ,∴点B的坐标为(
,∴点B的坐标为(![]() ) .
) .
(2) 将A(2,0)、B (![]() )、O(0,0)三点的坐标代入y=ax2+bx+c,得
)、O(0,0)三点的坐标代入y=ax2+bx+c,得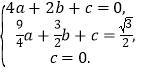
解有a=![]() ,b=
,b=![]() ,c="0." ∴所求二次函数解析式是 y=
,c="0." ∴所求二次函数解析式是 y=![]() x2+
x2+![]() x.
x.
(3) 设存在点C (x ,![]() x2+
x2+![]() x) (其中0<x<
x) (其中0<x<![]() ),使四边形ABCO面积最大.
),使四边形ABCO面积最大.
∵△OAB面积为定值,
∴只要△OBC面积最大,四边形ABCO面积就最大.
过点C作x轴的垂线CE,垂足为E,交OB于点F,则
S△OBC= S△OCF+S△BCF=![]() =
=![]() ,
,
而 |CF|=yC-yF=![]() ,
,
∴ S△OBC=![]() .
.
∴当x=![]() 时,△OBC面积最大,最大面积为
时,△OBC面积最大,最大面积为![]() .
.
此时,点C坐标为(![]() ),四边形ABCO的面积为
),四边形ABCO的面积为![]() .
.

【题目】根据扬州市某风景区的旅游信息,![]() 公司组织一批员工到该风景区旅游,支付给旅行社
公司组织一批员工到该风景区旅游,支付给旅行社![]() 元.
元. ![]() 公司参加这次旅游的员工有多少人?
公司参加这次旅游的员工有多少人?
扬州市某风景区旅游信息表
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加 |
【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共4个,某学习小组进行摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再放回,下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 33 | 60 | 130 | 202 | 251 |
摸到黑球的频率 |
|
|
|
|
|
|
![]() 当n很大时,估计从袋中摸出一个黑球的概率是______;
当n很大时,估计从袋中摸出一个黑球的概率是______;
![]() 试估算口袋中白球有______个;
试估算口袋中白球有______个;
![]() 在
在![]() 的条件下,若从中先换出一球,不放回,摇匀后再摸出一球,请用列表或树状图的方法求两次都摸到白球的概率.
的条件下,若从中先换出一球,不放回,摇匀后再摸出一球,请用列表或树状图的方法求两次都摸到白球的概率.