题目内容
已知a、b、c是一个三角形的三边,且方程a(x2-1)-2cx+b(x2+1)=0有两个相等的实数根,则该三角形是
- A.等腰三角形
- B.等边三角形
- C.直角三角形
- D.等腰直角三角形
C
分析:先把方程变形为一般形式:(a+b)x2-2cx-(a-b)=0,由方程有两个相等的实数根,得△=0,即△=4c2+4(a+b)(a-b)=4(a2+c2-b2)=0,由此得到a2+c2=b2,即可判断三角形的形状.
解答:方程化为一般形式为:(a+b)x2-2cx-(a-b)=0,
∵方程有两个相等的实数根,
∴△=0,即△=4c2-4(a+b)[-(a-b)]=4c2+4(a+b)(a-b)=4(a2+c2-b2)=0,
∴a2+c2=b2,
∴此三角形是以b为斜边的直角三角形.
故选C.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了勾股定理的逆定理.
分析:先把方程变形为一般形式:(a+b)x2-2cx-(a-b)=0,由方程有两个相等的实数根,得△=0,即△=4c2+4(a+b)(a-b)=4(a2+c2-b2)=0,由此得到a2+c2=b2,即可判断三角形的形状.
解答:方程化为一般形式为:(a+b)x2-2cx-(a-b)=0,
∵方程有两个相等的实数根,
∴△=0,即△=4c2-4(a+b)[-(a-b)]=4c2+4(a+b)(a-b)=4(a2+c2-b2)=0,
∴a2+c2=b2,
∴此三角形是以b为斜边的直角三角形.
故选C.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了勾股定理的逆定理.

练习册系列答案
相关题目
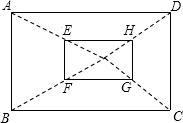 如图,已知长方形ABCD到长方形EFGH是一个相似变换,OA:OE=3:1.如果长方形ABCD的面积为9,那么,长方形EFGH的面积为
如图,已知长方形ABCD到长方形EFGH是一个相似变换,OA:OE=3:1.如果长方形ABCD的面积为9,那么,长方形EFGH的面积为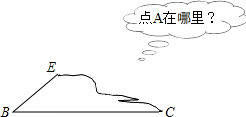 已知:如下图,原本是一个等腰三角形△ABC,其中,AB=AC,现在破损只剩下BC边和一个角∠B,你能帮助恢复原样吗?(要求:尺规作图,保留作图痕迹,不写作法,最后要作答)
已知:如下图,原本是一个等腰三角形△ABC,其中,AB=AC,现在破损只剩下BC边和一个角∠B,你能帮助恢复原样吗?(要求:尺规作图,保留作图痕迹,不写作法,最后要作答)