��Ŀ����
����Ŀ�����Dz���Լ������ֱ����ABC�У�����ϳ���ֱ�DZߵij���Ϊ�϶�ֱ�DZ߳��ȵ����������ֱ����ABCΪ�ƽ�������
��1����֪����O��0��0������A��2��0��������y���������ϵĵ������O����A���ɻƽ������ε�������������Ţ٣�0��1�����ڣ�0��2�����ۣ�0��3�����ܣ�0��4����
��2����֪��P��5��0�����ж�ֱ��y=2x-6�ڵ�һ�����Ƿ���ڵ�Q��ʹ����OPQ�ǻƽ������Σ������������Q�����꣬�������ڣ�˵�����ɣ�
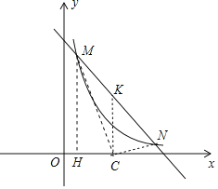
��3����֪������������![]() ��ֱ��y=-x+m+1����M��N���㣬����x��������ֻ��һ����C��ʹ�á�MCN=90
��ֱ��y=-x+m+1����M��N���㣬����x��������ֻ��һ����C��ʹ�á�MCN=90![]() ����m��ֵ�����жϴ�ʱ��MNC�Ƿ�Ϊ�ƽ������Σ�
����m��ֵ�����жϴ�ʱ��MNC�Ƿ�Ϊ�ƽ������Σ�
���𰸡���1���٢ܣ���2��Q����Ϊ��5��4������3���ǻƽ�������
��������
��1�����ݻƽ������εĶ��弴���жϣ�
��2��������ڣ���Q(m,2m6)�����������ηֱ���⼴�ɣ�
��3����M(x1,y1)��N(x2,y2)��MN���е�Ϊk������K��x��ľ������![]() ʱ����������������һԪ���η��̵ĸ���ϵ���Ĺ�ϵ�������������m�����жϣ�
ʱ����������������һԪ���η��̵ĸ���ϵ���Ĺ�ϵ�������������m�����жϣ�
�⣺��1����Ϊ��![]() ��0��0������
��0��0������![]() ��2��0�������ݻƽ������εĶ����֪��y���������ϵĵ�
��2��0�������ݻƽ������εĶ����֪��y���������ϵĵ�
��ԭ����߶γ���Ϊ1����4���ʽ����Ŀ��֪���![]() ����
����![]() ���ɻƽ������ε���
���ɻƽ������ε���![]() ��
��![]() ���ʴ�Ϊ�٢ܣ�
���ʴ�Ϊ�٢ܣ�
��2��������ڣ���![]() ��
��
![]() ��ֱ�������Σ���
��ֱ�������Σ���![]() ��ֱ��������ʱ��
��ֱ��������ʱ��![]() ��
��
![]() ����ã�
����ã�![]() ��4��
��4��
![]() ��
��![]() �ڵ�һ���ޣ�
�ڵ�һ���ޣ�![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() �ǻƽ������Σ�
�ǻƽ������Σ�
��![]() ʱ��
ʱ��![]() ����ʱ
����ʱ![]() ������ƽ������εĶ��壮
������ƽ������εĶ��壮
![]() �����������
�����������![]() ����Ϊ
����Ϊ![]() ��
��
��3����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���е�Ϊ
���е�Ϊ![]() ������
������![]() ��
��![]() ��ľ������
��ľ������![]() ʱ������������
ʱ������������
��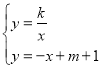 ����ȥ
����ȥ![]() �õ���
�õ���![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]()
![]() ��
��![]() ��
��![]()
![]() ��
��
�����ã�![]() ��
��![]() ��
��
��ͼ����![]() ����
����![]() ��
��
![]() ֱ��
ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ���ǻƽ������Σ�
���ǻƽ������Σ�