题目内容
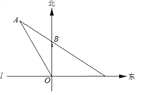
【题目】如图,在东西方向的海岸线上有一个码头M,在码头M的正西方向有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距![]() 千米的A处;经过3小时,又测得该轮船位于O的正北方向,且与O相距60千米的B处.
千米的A处;经过3小时,又测得该轮船位于O的正北方向,且与O相距60千米的B处.
(1)求该轮船航行的速度;
![]() (2)当该轮船到达B处时,一艘海监船从O点出发以每小时16千米的速度向正东方向行驶,请通过计算说明哪艘船先到达码头M.(参考数据:
(2)当该轮船到达B处时,一艘海监船从O点出发以每小时16千米的速度向正东方向行驶,请通过计算说明哪艘船先到达码头M.(参考数据: ![]() )
)
【答案】(1)20km/h;
(2)轮船先到
【解析】(1)过点A作AC⊥OB于点C.可知△ABC为直角三角形.根据勾股定理解答.
(2)分别计算两船的速度,比较大小即可得出结论.
【解答】解(1)过点A作AC⊥OB于点C.

由题意,得
OA=60![]() 千米,OB=60千米,∠AOC=30°.
千米,OB=60千米,∠AOC=30°.
∴AC=![]() OA=
OA=![]() ×60
×60![]() =30
=30![]() (千米).
(千米).
∵在Rt△AOC中,OC=OAcos∠AOC=60![]() ×
×![]() =90(千米).
=90(千米).
∴BC=OC-OB=90-60=30(千米).
∴在Rt△ABC中,AB=![]() (千米).
(千米).
∴轮船航行的速度为:60÷3=20(千米/时).
(2)由题意得:ΔABC∽ΔMBO
∴![]()
∴ BM=120千米,MO=60![]() 千米
千米
∴t轮船=120÷20=6h,t海监船=60![]() ÷16=
÷16=![]()
∵t轮船<t海监船
∴轮船先到

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目






