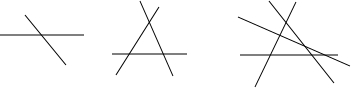题目内容
观察下列图形,并阅读图形下面的相关文字:
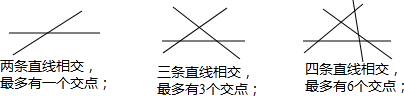
①两直线相交,最多1个交点;②三条直线相交最多有3个交点;③四条直线相交最多有6个交点;那么十条直线相交交点个数最多有( )
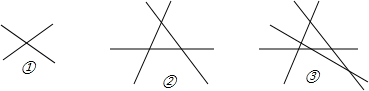
①两直线相交,最多1个交点;②三条直线相交最多有3个交点;③四条直线相交最多有6个交点;那么十条直线相交交点个数最多有( )

| A、40个 | B、45个 | C、50个 | D、55个 |
分析:根据题意,结合图形,发现:3条直线相交最多有3个交点,4条直线相交最多有6个交点,5条直线相交最多有10个交点.而3=1+2,6=1+2+3,10=1+2+3+4,故可猜想,n条直线相交,最多有1+2+3+…+(n-1)=
n(n-1)个交点.
| 1 |
| 2 |
解答:解:10条直线两两相交,最多有
n(n-1)=
×10×9=45.
故选B.
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:此题在相交线的基础上,着重培养学生的观察、实验和猜想、归纳能力,掌握从特殊向一般猜想的方法.

练习册系列答案
相关题目
观察下列图形,并阅读图形下方的相关文字(如图),
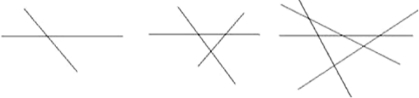
2条直线相交,3条直线相交,4条直线相交,
最多有1个交点;最多有3个交点;最多有6个交点.
像这样,50条直线相交,最多交点的个数有( )

2条直线相交,3条直线相交,4条直线相交,
最多有1个交点;最多有3个交点;最多有6个交点.
像这样,50条直线相交,最多交点的个数有( )
| A、1225 | B、1275 | C、2450 | D、2550 |