题目内容
解下列不等式,并把解集在数轴上表示出来:
(1)3(2x+2)≥4(x-1)+7.
(2)
-
>-2.
(1)3(2x+2)≥4(x-1)+7.
(2)
| x-1 |
| 3 |
| x+4 |
| 2 |
考点:解一元一次不等式,在数轴上表示不等式的解集
专题:计算题
分析:(1)去括号、然后移项、合并同类项、系数化成1即可求解;
(2)首先去分母,然后去括号、然后移项、合并同类项、系数化成1即可求解.
(2)首先去分母,然后去括号、然后移项、合并同类项、系数化成1即可求解.
解答:解:(1)去括号,得:6x+6≥4x-4+7,
移项,得:6x-4x≥-4+7-6,
合并同类项,得:2x≥-3,
系数化为1得:x≤-
,
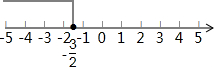 ;
;
(2)去分母,得:2(x-1)-3(x+4)>-12,
去括号,得:2x-2-3x-12>-12,
移项、合并同类项,得:-x>2,
系数化为1得:x<-2.
 .
.
移项,得:6x-4x≥-4+7-6,
合并同类项,得:2x≥-3,
系数化为1得:x≤-
| 3 |
| 2 |
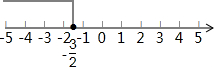 ;
;(2)去分母,得:2(x-1)-3(x+4)>-12,
去括号,得:2x-2-3x-12>-12,
移项、合并同类项,得:-x>2,
系数化为1得:x<-2.
 .
.点评:本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
相关题目
 如图所示,在△ABC中,∠ACB=90°,AD=AC,BE=BC,D、E两点在AB边上,
如图所示,在△ABC中,∠ACB=90°,AD=AC,BE=BC,D、E两点在AB边上, 尺规作图题:作∠DOE的平分线,并写出作法.
尺规作图题:作∠DOE的平分线,并写出作法. 如图,由4个全等的正方形组成的L形图案,请按下列要求画图:
如图,由4个全等的正方形组成的L形图案,请按下列要求画图: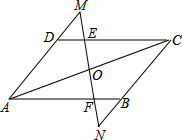 如图,O为?ABCD对角线AC的中点,过O点作一直线与DC、AB交于E、F,并与AD、CB的延长线分别交于M、N.求证:DM=BN.
如图,O为?ABCD对角线AC的中点,过O点作一直线与DC、AB交于E、F,并与AD、CB的延长线分别交于M、N.求证:DM=BN.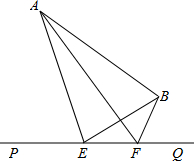 如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=60°,∠BEQ=45°;在点F处测得∠AFP=45°,∠BFQ=90°,EF=2km.
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=60°,∠BEQ=45°;在点F处测得∠AFP=45°,∠BFQ=90°,EF=2km.