��Ŀ����
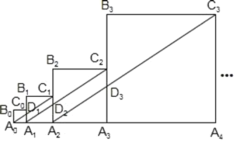
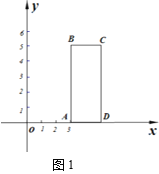
����Ŀ����ͼ1���ھ���ABCD�У�AB��5��AD��2����������x����������ϣ�AD��x���غ��ҵ�A����Ϊ(3��0)��
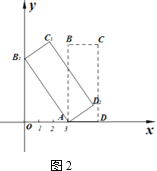
��1�����Ե�AΪ��ת���ģ�������ABCD��ʱ����ת��ʹ��B�䵽y���ϵĵ�B1�����õ�����AB1C1D1����ͼ2�����B1��C1��D1�����꣮
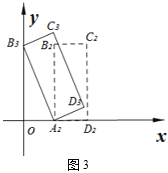
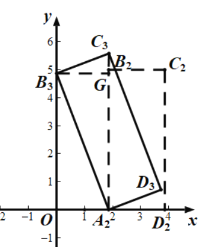
��2����������ABCD����ƽ��һ�ξ����õ�����A2B2C2D2����ͼ3���ٽ�����A2Ϊ��ת������ʱ����ת��ʹ��B2�䵽y���ϵĵ�B3������ʱ��C3ǡ�����ڵ�A2�����Ϸ��õ�����A2B3C3D3����ƽ�Ƶľ��벢д��C3�����꣮
���𰸡���1��B1(0��4)��![]() ��D1(4.6��1.2)����2��ƽ�Ƶľ��룺
��D1(4.6��1.2)����2��ƽ�Ƶľ��룺![]() ��C3(
��C3(![]() ��
��![]() )��
)��
��������
��1�������B1������Ϊ(0��4)����D1��D1E��x����E������Rt��AOB1��Rt��D1EA���ED1��1.2��EA��1.6�������ó�D1�����ꣻ����C1��C1F��y����F������Rt��B1C1F��Rt��AB1O���ó���C1B1F����B1AO���������Ǻ������![]() ��
��![]() ��ֵ�������ó�
��ֵ�������ó�![]() �����ꣻ
�����ꣻ
��2������B2C3������B3��B3G��A2C3��G����Rt��A2B3C3�����ù��ɶ������A2C3��ֵ�����õ���������![]() ��ֵ���Ӷ��ó�C3�����꣮
��ֵ���Ӷ��ó�C3�����꣮
�⣺��1����A(3��0)����OA��3��
��AB��5��������ת�����ʿ�֪AB1��AB��5��
��Rt��AOB1�У��ɹ��ɶ����ɵã�
OB1��![]() 4��
4��
��B1������Ϊ(0��4)��
����ͼ����D1��D1E��x����E��
���ı���AB1C1D1�Ǿ��Σ�
���B1AD1��90�㣬���OAB1����EAD1��90�㣬
�֡ߡ�OAB1����OB1A��90�㣬
���EAD1����OB1A��
�֡ߡ�AOB1����AED1��90�㣬
��Rt��AOB1��Rt��D1EA��
��![]() ��
��
����ת���ʿ�֪��AD1��AD��2��
��![]() ��
��
��ED1��1.2��EA��1.6��
��OE��OA��AE��3��1.6��4.6��
��D1(4.6��1.2)��
����C1��C1F��y����F��
ͬ���ɵã���Rt��B1C1F��Rt��AB1O��
���C1B1F����B1AO��
��![]()
��![]() ����
����![]() ��
��
��![]() �����
�����![]() ��
��
��![]() ��
��![]() ���
���![]()
��![]()
��![]() ��
��
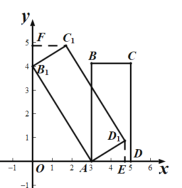
��2������B2C3������B3��B3G��A2C3��G��
��Rt��A2B3C3��A2B3��AB��5��B3C3��BC��2��
��A2C3��![]() ��
��
�֡�![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]()
�������ƽ�Ƶľ���Ϊ��![]() ��
��
��OA2��![]() ��A2C3��
��A2C3��![]()
���C3������Ϊ(![]() ��
��![]() )��
)��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�