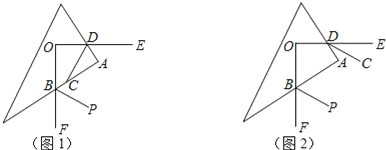��Ŀ����
����Ŀ����ͼ��ֱ��l��y=��x+1��x�ᣬy��ֱ���A��B���㣬��P��Q��ֱ��l�ϵ��������㣬�ҵ�P�ڵڶ����ޣ���Q�ڵ������ޣ���POQ=135�㣮
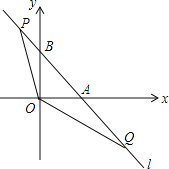
��1�����AOB���ܳ���
��2����AQ=t��0�����ú�t�Ĵ���ʽ��ʾ��P�����ꣻ
��3��������P��Q��ֱ��l���˶���ʹ�á�AOQ���BPO���ܳ����ʱ����tan��AOQ=m��������A�Ķ��κ���y=ax2+bx+cͬʱ������������������
��6a+3b+2c=0��
�ڵ�m��x��m+2ʱ������y�����ֵ����![]() ���������ϵ��a��ֵ��
���������ϵ��a��ֵ��
���𰸡���1����AOB�ܳ�Ϊ2+![]() ����2��P����
����2��P����![]() ��1+
��1+![]() ������3��a��ֵΪ
������3��a��ֵΪ![]() ��2
��2![]() ��2��
��2��
��������
�����������1�������A��B���꣬�����OB��OA��AB���ɽ�����⣮��2���ɡ�PBO�ס�OAQ����![]() =
=![]() �����PB���ٸ��ݵ���ֱ�����������ʿ�����õ�P���꣮��3�������m��ֵ���֢�a��0����a��0���������Σ����ö��κ������ʷֱ���⼴�ɣ�
�����PB���ٸ��ݵ���ֱ�����������ʿ�����õ�P���꣮��3�������m��ֵ���֢�a��0����a��0���������Σ����ö��κ������ʷֱ���⼴�ɣ�
�����������1���ں���y=��x+1�У���x=0����y=1��
��B��0��1����
��y=0����x=1��
��A��1��0����
��OA=OB=1��AB=![]() ��
��
���AOB�ܳ�Ϊ1+1+![]() =2+
=2+![]() ��
��
��2����OA=OB��
���ABO=��BAO=45�㣬
���PBO=��QAO=135�㣬
���POB=x�����OPB=��AOQ=135�㩁x��90��=45�㩁x��
���PBO�ס�OAQ��
��![]() =
=![]() ��
��
��PB=![]() =
=![]() ��
��
����P��PH��OB��H�㣬
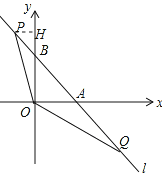
���PHBΪ����ֱ�������Σ�
��PB=![]() ��
��
��PH=HB=![]() ��
��
��P����![]() ��1+
��1+![]() ����
����
��3������2����֪��PBO�ס�OAQ�������ǵ��ܳ���ȣ������Ʊ�Ϊ1����ȫ�ȣ�
��PB=AQ��
��![]() =t��
=t��
��t��0��
��t=1��
ͬ���ɵ�Q��1+![]() ����
����![]() ����
����
��m=![]() =
=![]() ��1��
��1��
�������߾�����A��
��a+b+c=0��
�֡�6a+3b+2c=0��
��b=��4a��c=3a��
�Գ���x=2��ȡֵ��Χ![]() ��1��x
��1��x![]() +1��
+1��
����a��0�������ϣ�
������x=![]() ��1ʱȡ�����ֵ
��1ʱȡ�����ֵ![]() =2
=2![]() +2��
+2��
����![]() ��1��2a+��
��1��2a+��![]() ��1��b+c=2
��1��b+c=2![]() +2��
+2��
���a=![]() ��
��
����a��0�������£�
������x=2ʱȡ�����ֵ2![]() +2��
+2��
��4a+2b+c=2![]() +2��
+2��
���a=��2![]() ��2��
��2��
������������a��ֵΪ![]() ��2
��2![]() ��2��
��2��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�