题目内容
先观察下列等式,再完成题后问题:| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
(1)请你猜想:
| 1 |
| 2010×2011 |
(2)若a、b为有理数,且|a-1|+(ab-2)2=0,求:
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2009)(b+2009) |
分析:(1)根据
=
-
,
=
-
,
=
-
,…则
=
-
;
(2)先根据非负数的性质得出a、b的值,代入原式变形为 1-
+
-
+
-
…+
-
是解题的关键.
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2010×2011 |
| 1 |
| 2010 |
| 1 |
| 2011 |
(2)先根据非负数的性质得出a、b的值,代入原式变形为 1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2010 |
| 1 |
| 2011 |
解答:解:(1)
=
-
(2分)
(2)∵|a-1|+(ab-2)2=0,
∴a-1=0,ab-2=0,
∴a=1,b=2(2分)
原式=1-
+
-
+…+
-
(2分)
=
.(1分)
| 1 |
| 2010×2011 |
| 1 |
| 2010 |
| 1 |
| 2011 |
(2)∵|a-1|+(ab-2)2=0,
∴a-1=0,ab-2=0,
∴a=1,b=2(2分)
原式=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
| 1 |
| 2011 |
=
| 2010 |
| 2011 |
点评:考查了有理数的混合运算,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键规律为
=
-
.
| 1 |
| x(x+1) |
| 1 |
| x |
| 1 |
| x+1 |

练习册系列答案
相关题目
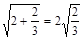 ; ②
; ②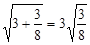 ;
;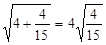 ; ④
; ④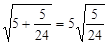
 ; ②
; ②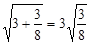 ;
; ; ④
; ④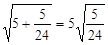
 ;
②
;
② ;
; ;
④
;
④