题目内容
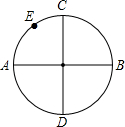
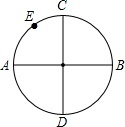如用，AB，CD是圆的两条互相垂直的直径，E是圆周上一点．在直径AB上找一点P，使PC+PE的最小的作法是连接DE，与AB的交点即为点P
连接DE，与AB的交点即为点P
．分析：根据AB⊥CD可知，点C与点D关于直线AB对称，故连接DE，DE与AB相交于点P，则点P即为所求点．
解答：解：∵AB⊥CD，
∴点C与点D关于直线AB对称，
∴连接DE，DE与AB相交于点P，则点P即为所求点．
故答案为：连接DE，与AB的交点即为点P．
∴点C与点D关于直线AB对称，
∴连接DE，DE与AB相交于点P，则点P即为所求点．
故答案为：连接DE，与AB的交点即为点P．
点评：本题考查的是轴对称-最短路线问题，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合本节所学轴对称变换来解决，多数情况要作点关于某直线的对称点．
练习册系列答案
相关题目
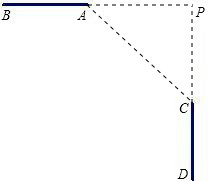在A、C两点处分别与道路相切），测得AC=60米，∠ACP=45度．
如用，AB，CD是圆的两条互相垂直的直径，E是圆周上一点．在直径AB上找一点P，使PC+PE的最小的作法是________．
