题目内容
如图,圆B切y轴于原点O,过定点A(-2| 3 |
 n∠PAB=
n∠PAB=
| ||
| 3 |
(1)求圆B的半径.
(2)若抛物线C经过点B,求其解析式.
(3)设抛物线C交y轴于点M,若三角形APM为直角三角形,求点M的坐标.
分析:(1)因为AP是⊙B的切线,所以连接PB可构造出直角三角形,利用直角三角形的性质及特殊角的三角函数值即可求出圆B的半径.
(2)根据⊙B的半径可求出B点坐标,利用勾股定理或切割线定理可求出AP的距离,根据AP、BP的长可求出P点坐标,再利用待定系数法即可求出二次函数的解析式.
(3)求出P点坐标和A点坐标,设出M点坐标为(0,t),根据勾股定理及其逆定理解答.
(2)根据⊙B的半径可求出B点坐标,利用勾股定理或切割线定理可求出AP的距离,根据AP、BP的长可求出P点坐标,再利用待定系数法即可求出二次函数的解析式.
(3)求出P点坐标和A点坐标,设出M点坐标为(0,t),根据勾股定理及其逆定理解答.
解答:解:
(1)连接PB,则PB⊥AP,设PB=r,
∵tan∠PAB=
,
∴∠PAB=30°,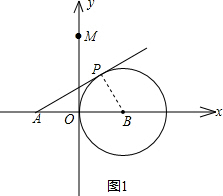
故r=
(OA+OB)=
(2
+r),
解得r=2
.
(2)如P在第一象限,OP与x轴的夹角=2∠PAB=60°
则:P点坐标(2
cos60°,2
sin60°),
即(
,3)
B、A关于y轴对称,所以抛物线顶点必在y轴上,
设为(0,m)
抛物线解析式:y-m=kx2
将(
,3),(2
,0),代入,
得:3-m=3k,-m=12k,m=4,k=-
抛物线解析式:y=-
x2+4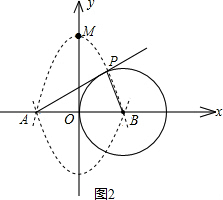
若P点在四象限,则:P点坐标(
,-3)
则抛物线解析式:y=-
x2-4
(3)由于P点坐标为(
,3),A点坐标为(-2
,0),M点坐标为(0,t).
根据勾股定理,①PA2=PM2+AM2,36=t2-6t+12+12+t2,
解得t=
;
②PM2=PA2+AM2,t2-6t+12=36+12+t2,解得t=-6;
③AM2=PA2+PM2,12+t2=36+t2-6t+12,解得t=6.
于是M点坐标为(0,-6),(0,6),(0,
),(0,
).
(1)连接PB,则PB⊥AP,设PB=r,
∵tan∠PAB=
| ||
| 3 |
∴∠PAB=30°,

故r=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
解得r=2
| 3 |
(2)如P在第一象限,OP与x轴的夹角=2∠PAB=60°
则:P点坐标(2
| 3 |
| 3 |
即(
| 3 |
B、A关于y轴对称,所以抛物线顶点必在y轴上,
设为(0,m)
抛物线解析式:y-m=kx2
将(
| 3 |
| 3 |
得:3-m=3k,-m=12k,m=4,k=-
| 1 |
| 3 |
抛物线解析式:y=-
| 1 |
| 3 |

若P点在四象限,则:P点坐标(
| 3 |
则抛物线解析式:y=-
| 1 |
| 3 |
(3)由于P点坐标为(
| 3 |
| 3 |
根据勾股定理,①PA2=PM2+AM2,36=t2-6t+12+12+t2,
解得t=
3±
| ||
| 2 |
②PM2=PA2+AM2,t2-6t+12=36+12+t2,解得t=-6;
③AM2=PA2+PM2,12+t2=36+t2-6t+12,解得t=6.
于是M点坐标为(0,-6),(0,6),(0,
3+
| ||
| 2 |
3-
| ||
| 2 |
点评:此题将圆、抛物线、直线结合起来,考查了对知识的综合运用能力.特别是解(3)时,要应用勾股定理进行分类讨论.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 P,使S四边形POCA=S△AOB?若存在,请直接写出点P的坐标;若不存在,请简要说明理由.
P,使S四边形POCA=S△AOB?若存在,请直接写出点P的坐标;若不存在,请简要说明理由. 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.

