题目内容
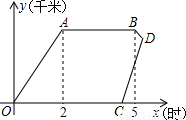
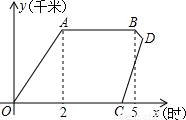
星期天,小强骑自行车到郊外与同学一起游玩,从家出发2小时到达目的地,游玩3小时后按原路以原速返回,小强离家4小时40分钟后,妈妈驾车沿相同路线迎接小强,如图,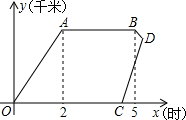 是他们离家的路程y(千米)与时间x(时)的函数图象.已知小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.
是他们离家的路程y(千米)与时间x(时)的函数图象.已知小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.(1)小强家与游玩地的距离是多少?
(2)妈妈出发多长时间与小强相遇?
分析:(1)直接利用时间乘以速度即可求得路程;
(2)分别求出直线BD,CD的解析式,联立方程组即可求得交点横坐标,即为相遇的时间.
(2)分别求出直线BD,CD的解析式,联立方程组即可求得交点横坐标,即为相遇的时间.
解答:解:(1)小强家与游玩地的距离是2×15=30千米;
(2)∵小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.
∴设yOA=15x,yBD=-15x+b1,yCD=60x+b2,
∵点B(5,30),点C(
,0),
则30=-15×5+b1,
解得b1=105,
0=60×
+b2,
解得b2=-280,
则yBD=-15x+105,yCD=60x-280,相遇即为-15x+105=60x-280,
解得x=5
,
5
-4
=
小时(即28分钟).
或设妈妈出发X时间与小强相遇,则
60x+15(x-
)=30,
解得x=
(即28分钟).
即妈妈出发28分钟与小强相遇.
(2)∵小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.
∴设yOA=15x,yBD=-15x+b1,yCD=60x+b2,
∵点B(5,30),点C(
| 14 |
| 3 |
则30=-15×5+b1,
解得b1=105,
0=60×
| 14 |
| 3 |
解得b2=-280,
则yBD=-15x+105,yCD=60x-280,相遇即为-15x+105=60x-280,
解得x=5
| 2 |
| 15 |
5
| 2 |
| 15 |
| 2 |
| 3 |
| 7 |
| 15 |
或设妈妈出发X时间与小强相遇,则
60x+15(x-
| 1 |
| 3 |
解得x=
| 7 |
| 15 |
即妈妈出发28分钟与小强相遇.
点评:主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义利用待定系数法准确的列出解析式,并会利用联立方程组的方法求交点坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
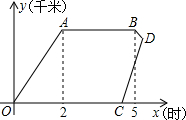 是他们离家的路程y(千米)与时间x(时)的函数图象.已知小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.
是他们离家的路程y(千米)与时间x(时)的函数图象.已知小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.