题目内容
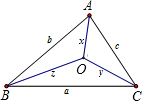 如图,温州鑫鑫打火机厂在厂房O的周围租了三幢楼A、B、C作为职工宿舍,每幢宿舍楼之间均有笔直的公路相连,并且厂房O与每幢宿舍楼之间也有笔直公路相连,且BC>AC>AB.厂房O到每条公路的距离相等.设BC=a,AC=b,AB=c,OA=x,OB=y,OC=z.现要用汽车每天接送职工上下班后,返回厂房停放,那么以下三条路线d1=x+c+a+z,d2=x+b+a+y,d3=y+c+b+z最短的是
如图,温州鑫鑫打火机厂在厂房O的周围租了三幢楼A、B、C作为职工宿舍,每幢宿舍楼之间均有笔直的公路相连,并且厂房O与每幢宿舍楼之间也有笔直公路相连,且BC>AC>AB.厂房O到每条公路的距离相等.设BC=a,AC=b,AB=c,OA=x,OB=y,OC=z.现要用汽车每天接送职工上下班后,返回厂房停放,那么以下三条路线d1=x+c+a+z,d2=x+b+a+y,d3=y+c+b+z最短的是A、d1;B、d2;C、d3;D、三条路线一样长;E、d1=d2且为最短路线;F、d1=d3且为最短路线.
分析:首先得出O为△ABC的内心,进而得出△ABO≌△EBO(SAS),在△ECO中,y-x<a-b推出d3-d1<0,同理d3-d2<0,即可得出答案.
解答: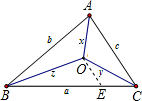 解:∵厂房O到每条公路的距离相等,
解:∵厂房O到每条公路的距离相等,
∴O为△ABC的内心,
∵在BC上截取BE=BA,连接OE,
在△ABO和△EBO中,
∴△ABO≌△EBO(SAS),
∴OA=OE,
在△ECO中,
y-x<a-b推出d3-d1<0,
同理d3-d2<0,
∴d3最短,
故选C.
 解:∵厂房O到每条公路的距离相等,
解:∵厂房O到每条公路的距离相等,∴O为△ABC的内心,
∵在BC上截取BE=BA,连接OE,
在△ABO和△EBO中,
|
∴△ABO≌△EBO(SAS),
∴OA=OE,
在△ECO中,
y-x<a-b推出d3-d1<0,
同理d3-d2<0,
∴d3最短,
故选C.
点评:本题考查了三角形的内切圆和内心,三角形的三边关系定理:两边之和大于第三边;以及在同一个三角形内大角对大边.

练习册系列答案
相关题目
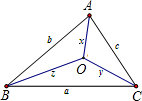 如图,温州鑫鑫打火机厂在厂房O的周围租了三幢楼A、B、C作为职工宿舍,每幢宿舍楼之间均有笔直的公路相连,并且厂房O与每幢宿舍楼之间也有笔直公路相连,且BC>AC>AB.厂房O到每条公路的距离相等.设BC=a,AC=b,AB=c,OA=x,OB=y,OC=z.现要用汽车每天接送职工上下班后,返回厂房停放,那么以下三条路线d1=x+c+a+z,d2=x+b+a+y,d3=y+c+b+z最短的是________
如图,温州鑫鑫打火机厂在厂房O的周围租了三幢楼A、B、C作为职工宿舍,每幢宿舍楼之间均有笔直的公路相连,并且厂房O与每幢宿舍楼之间也有笔直公路相连,且BC>AC>AB.厂房O到每条公路的距离相等.设BC=a,AC=b,AB=c,OA=x,OB=y,OC=z.现要用汽车每天接送职工上下班后,返回厂房停放,那么以下三条路线d1=x+c+a+z,d2=x+b+a+y,d3=y+c+b+z最短的是________