题目内容
【题目】如图△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,给出下列结论:①DC=DE;②DA平分∠CDE;③DE平分∠ADB;④BE+AC=AB;⑤∠BAC=∠BDE.其中正确的是_____ (写序号)
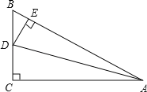
【答案】①②④⑤
【解析】
根据角平分线上的点到角的两边的距离相等可得DC=DE,判断①正确,然后利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应角相等可得∠ADC=∠ADE,判断②正确;全等三角形对应边相等可得AC=AE,然后求出BE+AC=AB,判断④正确;根据同角的余角相等求出∠BAC=∠BDE,判断⑤正确,并得到③错误.
解:∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴DC=DE,故①正确;
在Rt△ACD和Rt△AED中,![]() ,
,
∴Rt△ACD≌Rt△AED(HL),
∴∠ADC=∠ADE,AC=AE,
∴DA平分∠CDE,故②正确;
BE+AC=BE+AE=AB,故④正确;
∵∠BAC+∠B=90°,
∠BDE+∠B=90°,
∴∠BAC=∠BDE,故⑤正确;
∵∠ADE+∠BAD=90°,而∠BAD≠∠B,
∴∠BDE≠∠ADE,
∴DE平分∠ADB错误,故③错误;
综上所述,正确的有①②④⑤.
故答案为:①②④⑤.

 阅读快车系列答案
阅读快车系列答案【题目】某商场购进一批 30 瓦的 LED 灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED 灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |

(1)该商场购进了 LED 灯泡与普通白炽灯泡共 300 个,LED 灯泡按标价进行销售,而普通 白炽灯泡打九折销售,当销售完这批灯泡后可获利 3 200 元,求该商场购进 LED 灯泡与 普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进这两种灯泡 120 个, 在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的 30%, 并求出此时这批灯泡的总利润为多少元?