Question

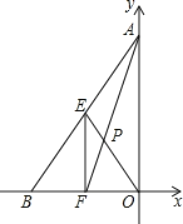
【题目】如图，在平面直角坐标系中，O为坐标原点，点A，B的坐标分别为（0，4），（﹣3，0），E为AB的中点，EF∥AO交OB于点F，AF与EO交于点P，则EP的长为_____．

Answer 1

【答案】.

【解析】

由点A，B的坐标可得出OA，OB的长度，根据三角形的中位线可得出EF，OF的长，在Rt△OEF中，利用勾股定理可得出OE的长，由EF∥AO可得出△EPF∽△OPA，利用相似三角形的性质可得出 ，结合EP+OP= 即可求出EP的长．

解：∵点A，B的坐标分别为（0，4），（﹣3，0），

∴OA＝4，OB＝3．

∵E为AB的中点，EF∥AO交OB于点F，

∴EF＝OA＝2，OF＝OB＝．

在Rt△OEF中，OF＝，EF＝2，

∴OE＝．

∵EF∥AO，

∴△EPF∽△OPA，

∴，

∴，

∴EP＝OE＝．

故答案为：．