题目内容
观察下面三行数:
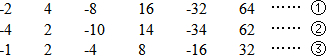
(1)填空:第二行第9个数为
(2)是否存在这样一列,使得其中三个数和为638?若存在,求这三个数;若不存在,说明理由.
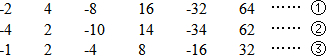
(1)填空:第二行第9个数为
-514
-514
;(2)是否存在这样一列,使得其中三个数和为638?若存在,求这三个数;若不存在,说明理由.
分析:(1)利用第一行已知数据得出数字变化规律进而得出第二行规律求出即可;
(2)利用已知规律得出三行数据的规律进而得出方程求出即可.
(2)利用已知规律得出三行数据的规律进而得出方程求出即可.
解答:解:(1)∵-2,4,-8,16,-32,64,…
∴第n个数为:(-1)n×2n,
∵第二行每个数都比第一行每个数小2,
∴第二行第9个数为:(-1)n×2n-2=(-1)9×29-2=-514;
故答案为:-514;
(2)∵-1,2,-4,8,-16,32…
∴第n个数为:(-1)n×2n-1,
∴第三行是第一行的一半,
∴设第一行第一个数为x,则x+x-2+
=638.
解得:x=256,
∵28=256,
∴存在这样一列,使得其中三个数和为638.
∴第n个数为:(-1)n×2n,
∵第二行每个数都比第一行每个数小2,
∴第二行第9个数为:(-1)n×2n-2=(-1)9×29-2=-514;
故答案为:-514;
(2)∵-1,2,-4,8,-16,32…
∴第n个数为:(-1)n×2n-1,
∴第三行是第一行的一半,
∴设第一行第一个数为x,则x+x-2+
| x |
| 2 |
解得:x=256,
∵28=256,
∴存在这样一列,使得其中三个数和为638.
点评:此题主要考查了数字变化规律,利用已知得出数字的变与不变是解题关键.

练习册系列答案
相关题目