题目内容
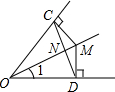
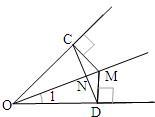10、如图，点M为∠COD的角平分线上一点，过点M作MC⊥OC于点C，MD⊥OD于点D，连接CD交OM于点N，则下列结论：①MC=MD，②∠CMO=∠DMO，③OM⊥CD，且NC=ND，④若∠1=30°，则OD=2MD，正确的有（ ）分析：利用∠COD关于角平分线的性质进行思考，得出结论后与所给出的项进行比对，选择符合要求的．
解答：解：∵点M为∠COD的角平分线上一点，过点M作MC⊥OC于点C，MD⊥OD于点D，
∴MC=MD，
∴△OMC≌△OMD，
∴∠CMO=∠DMO，
∴△ONC≌△OND，
∴∠ONC=∠OND=90°，
即OM⊥CD．
∴①②③对．
④应为若∠1=30°，则OM=2MD，故本选项错误．
故选A．
∴MC=MD，
∴△OMC≌△OMD，
∴∠CMO=∠DMO，
∴△ONC≌△OND，
∴∠ONC=∠OND=90°，
即OM⊥CD．
∴①②③对．
④应为若∠1=30°，则OM=2MD，故本选项错误．
故选A．
点评：本题主要考查了角平分线上的一点到两边的距离相等的性质；做题时，要对选项逐个验证．找准全等三角形是正确解决本题的关键．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
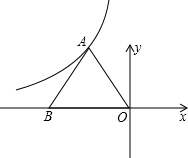
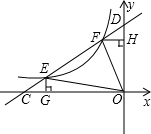
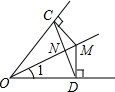如图，点M为∠COD的角平分线上一点，过点M作MC⊥OC于点C，MD⊥OD于点D，连接CD交OM于点N，则下列结论：①MC=MD，②∠CMO=∠DMO，③OM⊥CD，且NC=ND，④若∠1=30°，则OD=2MD，正确的有