题目内容
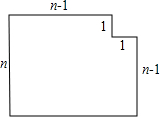 如图,设n是大于1的自然数,从n×n的正方形的一个角上剪去一个1×1的方块将这个图形分成k个面积都相等的三角形,试求k的最小值.
如图,设n是大于1的自然数,从n×n的正方形的一个角上剪去一个1×1的方块将这个图形分成k个面积都相等的三角形,试求k的最小值.
分析:先根据所给的正方形及三角形的面积公式确定三角形的面积,根据n的取值范围可确定出k的最值.
解答: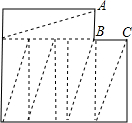 解:如图,在同折线ABC有公共点这些等积三角形中,必有一三角形的一边是AB(或BC)的一部分,这条边长度不大于1,而这条边上的高不大于n-1,所该三角形面积超过
解:如图,在同折线ABC有公共点这些等积三角形中,必有一三角形的一边是AB(或BC)的一部分,这条边长度不大于1,而这条边上的高不大于n-1,所该三角形面积超过
;另一方面,这个三角形面积等于
;故
≤
,
由此可知k≥2n+2.
综上所述,k的最小值是2n+2.
 解:如图,在同折线ABC有公共点这些等积三角形中,必有一三角形的一边是AB(或BC)的一部分,这条边长度不大于1,而这条边上的高不大于n-1,所该三角形面积超过
解:如图,在同折线ABC有公共点这些等积三角形中,必有一三角形的一边是AB(或BC)的一部分,这条边长度不大于1,而这条边上的高不大于n-1,所该三角形面积超过| n-1 |
| 2 |
| n2-1 |
| k |
| n2-1 |
| k |
| n-1 |
| 2 |
由此可知k≥2n+2.
综上所述,k的最小值是2n+2.
点评:本题考查的是一元一次不等式的解法及三角形的面积公式,根据题意确定出三角形的边长是解答此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目


 如图,设n是大于1的自然数,从n×n的正方形的一个角上剪去一个1×1的方块将这个图形分成k个面积都相等的三角形,试求k的最小值.
如图,设n是大于1的自然数,从n×n的正方形的一个角上剪去一个1×1的方块将这个图形分成k个面积都相等的三角形,试求k的最小值.