Question

如图，A处为牧草地，B处是牧童的家，A，B两处距河岸的距离分别为AC=350m，BD=1250m，且AB两地的距离为1500m，天黑前牧童从A点将马牵到河边去饮水，再赶回家．为了使所走的路程最短，牧童应将马赶到河边的什么地点？请你在图中画出来；请你求出他要走的最短路程．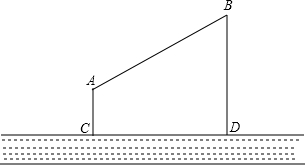

Answer 1

分析：要求牧民行驶距离最短的饮水点P，除非AP、BP的和为两定点之间的距离，也即是P在两定点F、B的连线上．根据勾股定理求出FB的长．

解答：解：（1）作点A关于CD的对称点F，连接BF交CD于点P，则点P为所求．

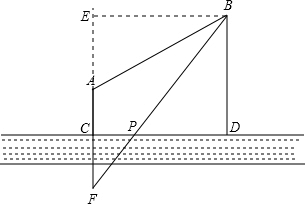
（2）作BE⊥BD交CA的延长线于点E，如图所示，
由题意得AE=1250-350=900m，EF=1250+350=1600
由勾股定理得：BE=

15002-9002

=1200
由勾股定理得：BF=

12002+16002

=2000
所以最短路程为2000米．

点评：本题考查了最短路径的数学问题．这类问题的解答依据是“两点之间，线段最短”，可以利用对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离．