��Ŀ����
����Ŀ����ͼ������ABC�У���C=90����AC=BC=4��D��AB���е㣬��E��F�ֱ���AC��BC�����˶�����E�����A��C�غϣ����ұ���AE=CF������DE��DF��EF���ڴ��˶��仯�Ĺ����У������н��ۣ�
�١�DFE�ǵ���ֱ�������Σ�
���ı���CEDF������Ϊ�����Σ�
���ı���CEDF��������Eλ�õĸı�������仯��
����C���߶�EF��������Ϊ![]() ��
��
������ȷ���۵ĸ����ǣ� ��

A.1��B.2��C.3��D.4��
���𰸡�B
��������
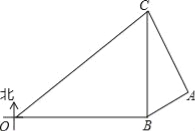
������CD����ͼ1����
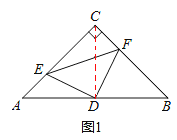
�ߡ�ABC�ǵ���ֱ�������Σ����DCB=��A=45����CD=AD=DB��
��AE=CF�����ADE�ա�CDF��SAS����
��ED=DF����CDF=��EDA��
�ߡ�ADE+��EDC=90�������EDC+��CDF=��EDF=90����
���DFE�ǵ���ֱ�������Ρ�
�ʴ˽�����ȷ��
����E��F�ֱ�ΪAC��BC�е�ʱ��������������λ�߶�����DEƽ���ҵ���![]() BC��
BC��
���ı���CEDF��ƽ���ı��Ρ�
����E��F�ֱ�ΪAC��BC�е㣬AC=BC�����ı���CEDF�����Ρ�
���ߡ�C=90�������ı���CEDF�������Ρ�
�ʴ˽��۴���
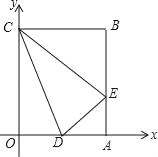
����ͼ2���ֱ����D����DM��AC��DN��BC���ڵ�M��N��
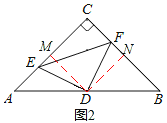
������֪�ı���CMDN�������Σ���DM=DN��
������֪��DFE�ǵ���ֱ�������Σ���DE=DF��
��Rt��ADE��Rt��CDF��HL����
���ɸ����֪�ı���CEDF���������������CMDN�����
���ı���CEDF����������Eλ�õĸı�������仯��
�ʴ˽��۴���
����������DEF�ǵ���ֱ�������Σ���FE=![]() DF��
DF��
��DF��BC��ֱ����DF��Сʱ�� EFȡ��Сֵ2![]() ����ʱ��C���߶�EF��������Ϊ
����ʱ��C���߶�EF��������Ϊ![]() ��
��
�ʴ˽�����ȷ��
����ȷ����2�����٢�����ѡB��
���ڴ�������⣡

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ijУ����ȫ��ѧ����������д��������ÿλѧ����д����39��![]() �����ȡ�˲���ѧ������д��������Ƴ����µ�ͼ����
�����ȡ�˲���ѧ������д��������Ƴ����µ�ͼ����
��� | ��ȷ����x | ���� |
A |
| 10 |
B |
| 15 |
C |
| 25 |
D |
| m |
E |
| n |
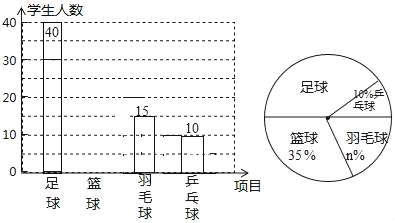
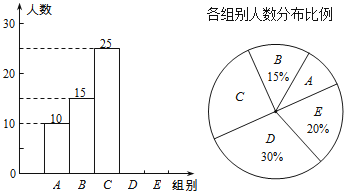
����������Ϣ����������⣺
![]() ͳ�Ʊ��е�
ͳ�Ʊ��е�![]() ______��
______��![]() ______������ȫ����ͳ��ͼ��
______������ȫ����ͳ��ͼ��
![]() ����ͳ��ͼ����C��������Ӧ��Բ�ĽǵĶ�����______��
����ͳ��ͼ����C��������Ӧ��Բ�ĽǵĶ�����______��
![]() ��֪��У����900��ѧ���������д��ȷ���ֵĸ�������24����Ϊ���ϸ�������Ƹ�У������д�������ϸ��ѧ��������
��֪��У����900��ѧ���������д��ȷ���ֵĸ�������24����Ϊ���ϸ�������Ƹ�У������д�������ϸ��ѧ��������
����Ŀ��Ŀǰ���ܵ��ڸ������ѻ����ռ�������ij�������ؼ���ũ������ƹ㣬Ϊ��Ӧ���٣����������̳�����![]() Ԫ�������ͺ��������ֽ��ܵƣ��������ͺŽ��ܵƵĽ��ۡ��ۼ����:
Ԫ�������ͺ��������ֽ��ܵƣ��������ͺŽ��ܵƵĽ��ۡ��ۼ����:
���ۣ�Ԫ/ֻ�� | �ۼۣ�Ԫ/ֻ�� | |
���� |
|
|
���� |
|
|
�ر�˵����ë����=�ۼ�-���ۣ�
��1�����������̳����ۼ��ͽ��ܵ�һֻë������______Ԫ��
��2��������������̳�����ף������ֽ��ܵƹ�![]() ֻ���������˼��ͽ��ܵƶ���ֻ?
ֻ���������˼��ͽ��ܵƶ���ֻ?
��3�����ڳ��������̳��������ͽ��ܵ�![]() ֻ����������̳�����һ����������ܵ�ʱ�����ë�����Ƕ���?
ֻ����������̳�����һ����������ܵ�ʱ�����ë�����Ƕ���?